Scaling Offline Reinforcement Learning at Test Time
July 14, 2025This research introduces a novel approach to scaling reinforcement learning (RL) during training and inference. Inspired by the recent work on LLM test-time scaling, we demonstrate how greater test-time compute can be leveraged to improve the performance of expressive, flow-based policies in RL.
“One thing that should be learned… is the great power of general purpose methods, of methods that continue to scale with increased computation even as the available computation becomes very great. The two methods that seem to scale arbitrarily… are search and learning.”
–Richard Sutton’s “The Bitter Lesson”
Reinforcement learning (RL) is a powerful paradigm for training agents to make sequential decisions. It has been successfully applied to fine-tuning large language models (LLMs), achieved superhuman performance in Go, Chess, and video games, and was recognized by the 2024 ACM A.M. Turing Award. However, despite its promising successes in these applications, RL has yet to become widely adopted in real-world robotics, primarily due to its lack of scalability.
Online RL requires an agent to interact with an environment. In board and video games, these interactions can be performed efficiently and safely through the game’s simulator, but robots interact with the real world. While online RL’s sample inefficiency can be overcome in simulation through parallelization, collecting the necessary data (i.e., interactions) on a real-world robot is often infeasible due to safety concerns (e.g., autonomous vehicles) and time and resource constraints (e.g., a home robot putting away dishes).
Instead, we seek a scalable RL-based approach to training robots. A promising alternative is to leverage offline RL, which aims to train agents from fixed, often sub-optimal datasets without interaction—eliminating the safety and resource constraints of environment interaction during online RL’s training. In this blog post, we will discuss what it takes to scale offline RL in robotics. In particular, we frame the discussion around the three primary axes of scaling that have proved most effective in the recent advances in machine learning. Specifically, the axes leverage:
- Large-scale data,
- Models with greater capacity, and
- Greater computation.
1. Scaling Data. Offline RL algorithms learn from a fixed dataset of interactions. In robotics, the data may come from different robots performing a variety of tasks at varying levels of competency. In contrast to the high-quality datasets used in imitation learning, offline RL can leverage sub-optimal and diverse data — for example, data from different robots that perform tasks in different ways, complete sub-tasks in varying orders, or fail to complete tasks. Thus, offline RL algorithms must be capable of handling large, diverse multi-modal datasets.


Figure 1: Sub-tasks in long-horizon problems can be accomplished in different orders.
2. Scaling Models. In order to handle large, diverse datasets, offline RL algorithms must leverage powerful and expressive models (e.g., diffusion and flow models), which (unlike standard Gaussian-based policy classes) are capable of modeling complex data distributions. However, while these powerful generative models are highly expressive, applying them to offline RL is challenging due to their iterative noise sampling process, which makes policy optimization difficult, as they often require extensive backpropagation through time. Ultimately, we seek a training procedure that can efficiently train an expressive model class on large, diverse data.
3. Test-Time Scaling. To date, prior work in offline RL has focused on training-time, specifically improvements along the axes of data and models. However, recent work in LLMs has demonstrated impressive performance gains from test-time scaling: clever ways of leveraging additional test-time compute. Inspired by this work, we investigate how this third axis of greater computation at test time can be applied in offline RL with generative models. That is, we seek an approach that can both perform inference efficiently (e.g., for the anytime inference necessary in autonomous vehicles) and leverage additional test-time compute when available (e.g., in surgical robots).
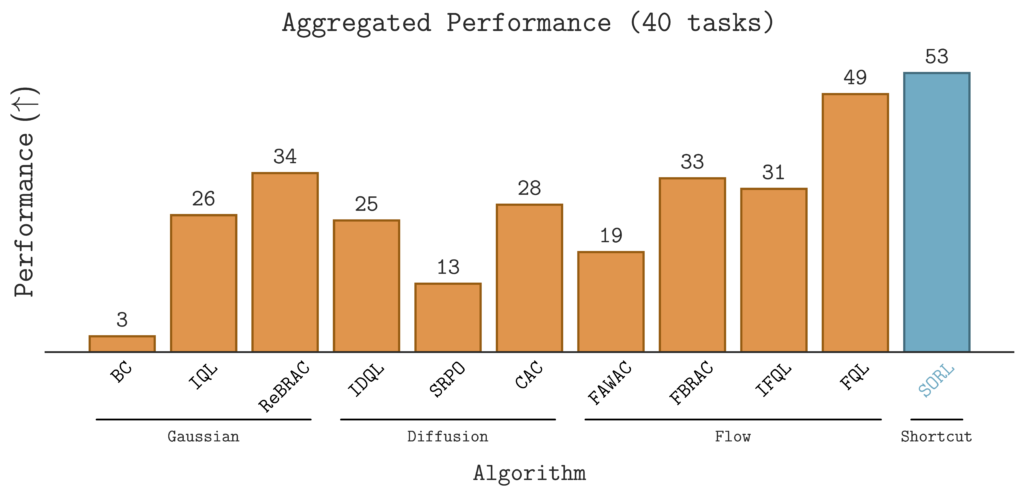
Scaling Offline Reinforcement Learning. The question, of course, is how we tackle scaling along all three axes. To accomplish this, we first leverage shortcut models, a new class of generative model, to train an efficient and expressive policy. We then introduce methods for sequential and parallel scaling that improve performance and enable sequential extrapolation. Overall, our method demonstrates the best performance against 10 baselines on 40 offline RL tasks.
Unlocking Efficiency and Expressivity with Shortcut Models
At a high level, generative models like flow matching sample actions by starting with some Gaussian noise and iteratively denoising it.
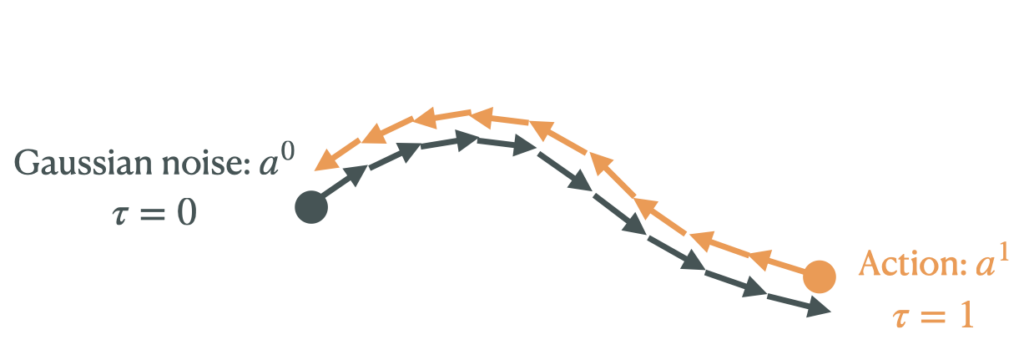
This iterative sampling process makes policy optimization difficult, since policy optimization often requires computing the gradient of the policy $\pi_\theta$ or $Q$-function with respect to an action (i.e., $\frac{\partial Q}{\partial \theta}$). More specifically, given $Q(s, a^1)$, we need to optimize $\theta$ via backpropagation through time (BPTT)
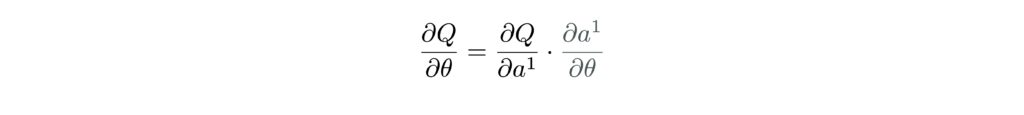
To remedy this problem, we use a new class of generative models, known as shortcut models (Frans et al., “One Step Diffusion via Shortcut Models”), that learn to make larger “jumps” in the denoising process, thus enabling efficient and expressive inference. For example, a shortcut model can replace the 9-step denoising procedure with a 2 or 3-step procedure.
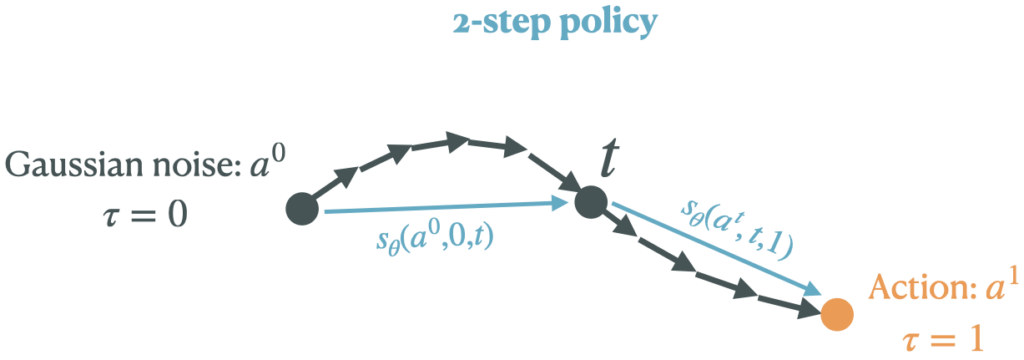
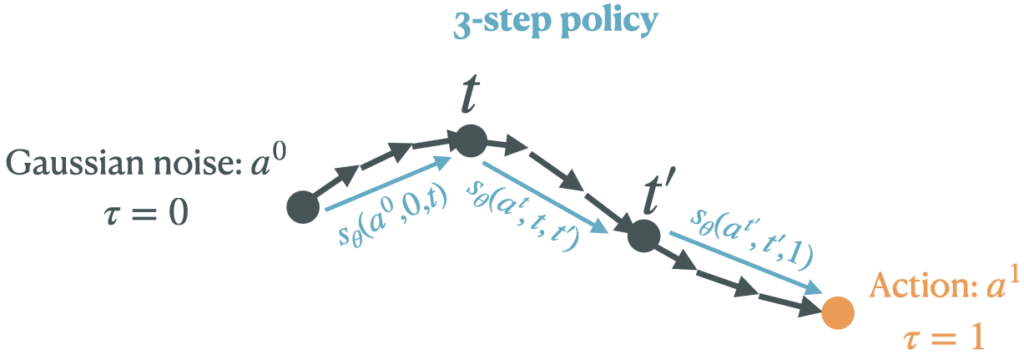
We can define the shortcut model by $$s_\theta(a^{t}, t, t’)$$ where $t$ is the starting timestep (in the noising process), $a^t$ is the noised action at the timestep $t$, and $t’$ is the timestep that the shortcut model jumps to. For clarity, we simplify the notation slightly in this post.
With shortcut models, instead of having to optimize the $Q$-function by backpropagating through all the discretization steps, we can instead sample an action via a short $M$-step procedure (e.g., 1 or 2 steps), which makes backpropagation through time in the ordinary differential equation (ODE) reasonable to compute.
Connection to Flow Models. If the shortcut model’s jump size is shrunk so that $t’-t \to 0$, the shortcut model $s_\theta(a^{t}, t, t’)$ recovers the instantaneous velocity field of a flow matching model. Chaining the infinitesimal shortcuts reconstructs the standard flow ODE. Conversely, by learning to take larger jumps while enforcing self-consistency among the jumps, the shortcut model decreases the computation required for action generation.
Scalable Offline RL ($\texttt{SORL}$)
At a high level, $\texttt{SORL}$ follows the following procedure:
1. Train $Q^{\pi_{\theta}}$ with standard offline methods (i.e., Bellman error minimization), and
2. Train the policy (i.e., the shortcut model) with regularization by:

Policy Optimization. The challenging part of training RL with generative models efficiently is the policy optimization component. Policy optimization typically requires computing the gradient of the policy, but the policy is a generative model that uses an iterative noise sampling process. To maintain efficiency, we perform policy optimization by sampling actions from the shortcut model using its “jumps”. Since the number of jumps is small—we experiment with $M=1, 2, 4, 8$—we can backpropagate the $Q$ loss efficiently. In other words, even though sampling $a \sim \pi_{\theta}$ may involve multi-step generations, the gradient of the loss function, $\nabla_\theta \mathcal{L}$, is still computable.
Regularization to Offline Data. To keep the policy inside the support of the offline data and thus avoid distribution shift between the training distribution (i.e., the offline data) and the test-time distribution (i.e., the distribution encountered by the learned policy), we add a behavioral cloning-style regularization between the learned policy $\pi$ and the offline data-generating policy, $\pi_B$.
Self-Consistency. Finally, we enforce that a single large jump should agree with the composition of two smaller ones. Concretely, the self-consistency loss matches the output of an $m$-step shortcut to the result of two consecutive $m/2$-step shortcuts. Informally, self-consistency ensures that
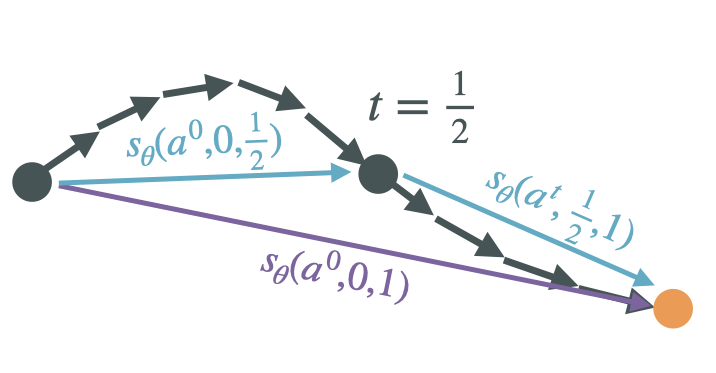
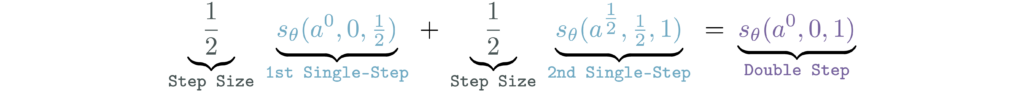
Self-consistency allows us to perform policy optimization with fewer backpropagation steps through time, while still regularizing using a greater number of discretization steps and ensuring all-step procedures are a reasonable approximation of the ODE.
$\texttt{SORL}$ Outperforms 10 Baselines on 40 Tasks
To evaluate $\texttt{SORL}$, we benchmark it against 10 offline RL baselines on 40 diverse tasks in the OG Bench Library. These tasks span locomotion (e.g., $\texttt{humanoidmaze}$, $\texttt{antmaze}$), long-horizon manipulation tasks (e.g., $\texttt{scene-play}$), and sparse-reward environments (e.g., $\texttt{antsoccer-arena}$).The results are summarized in the table below.
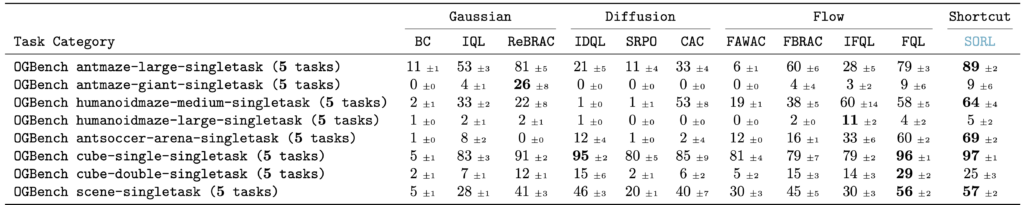
Notably, $\texttt{SORL}$ demonstrates strong improvements in challenging, sparse-reward environments.
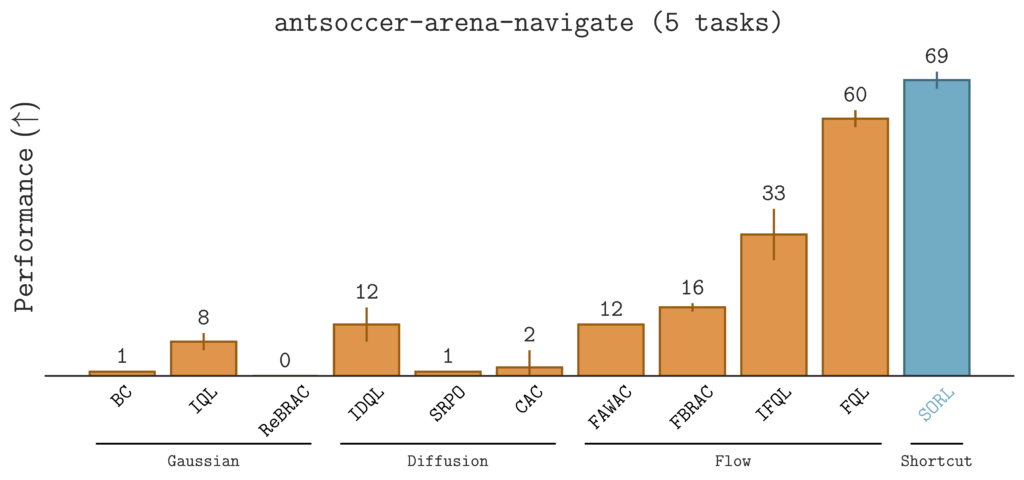
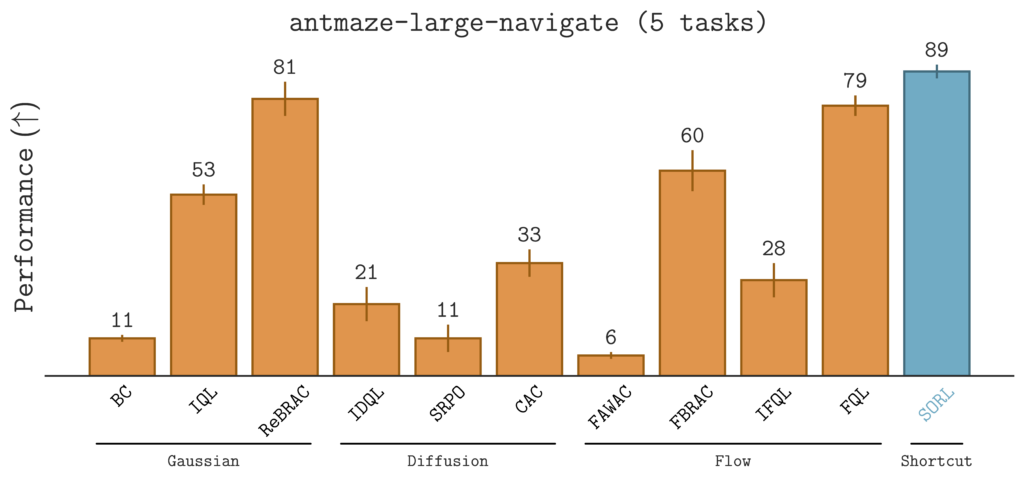
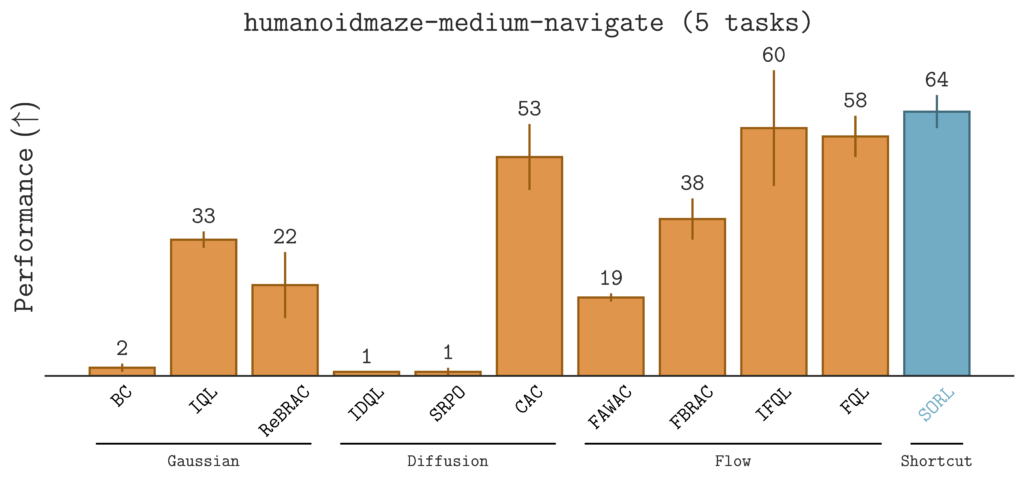
Qualitatively, $\texttt{SORL}$ generally learns smooth behaviors across a wide range of scenarios, from dexterous manipulation to agile locomotion:






Figure 5: cube-single-play, cube-double-play, scene-play, antsoccer-arena-navigate, antmaze-large-navigate, humanoidmaze-medium-navigate
Inference-Time Scaling
Performance Improvement Through Sequential Scaling
A key benefit of $\texttt{SORL}$ is that we have a simple way to perform sequential test-time scaling: increase the number of inference steps used to sample an action. Enforcing self-consistency during training enables flexible inference with a variable number of steps at test time, meaning we can choose the number of inference steps without having to retrain the policy. Using a larger number of steps enables the policy to model richer distributions and decrease the approximation error.
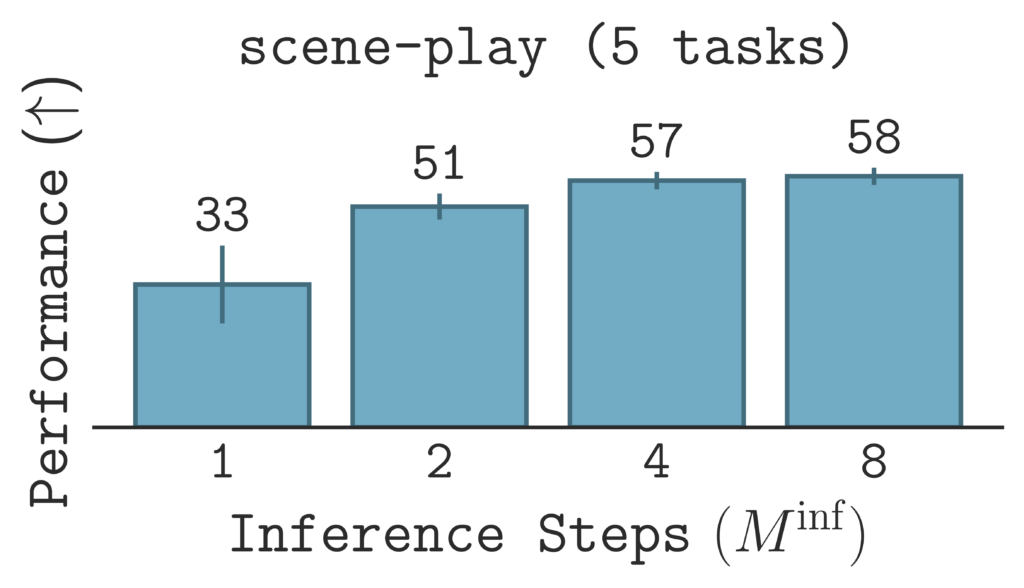
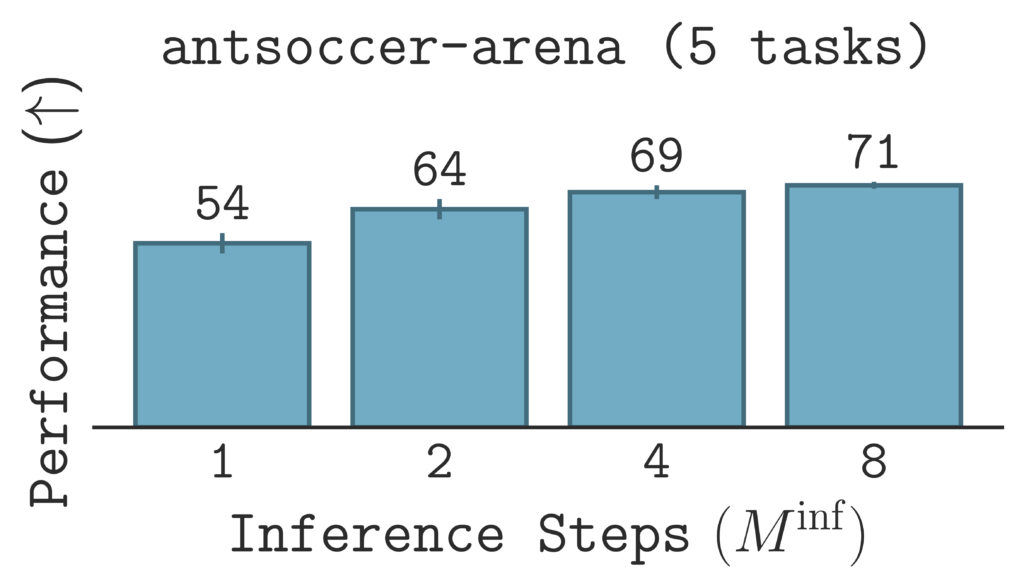
For a fixed training budget, $\texttt{SORL}$’s performance generally improves by increasing the number of inference steps at test time.
We investigate $\texttt{SORL}$’s sequential scaling by plotting the results of varying inference steps given the same, fixed training budget. The results show improvement in performance as the number of inference steps increases, suggesting that $\texttt{SORL}$ scales positively with greater test-time compute.
Qualitatively, sequential scaling leads to more precise actions.
On $\texttt{antsoccer}$ tasks, the 1-step policy struggles to reach the goal reliably, while the 8-step policy smoothly navigates to the target.


Figure 6: 1-step policy (left) struggles close to goal, whereas 8-step policy (right) reaches goal smoothly. (A subset of the trajectory is shown.)
On $\texttt{scene}$ manipulation tasks, the 1-step policy pushes the handle, while the 8-step policy grips the handle.


Figure 7: 1-step policy (left) pushes handle, whereas 8-step policy (right) grips handle.
In long-horizon environments like $\texttt{scene}$, the 8-step policy is better able to compose multiple sub-tasks, whereas the 1-step policy stalls or executes sub-optimal sequences.


Figure 8: 1-step policy (left) struggles to close the drawer, whereas 8-step policy (right) solves the sub-tasks smoothly.
Sequential Extrapolation Through Parallel Scaling
We also seek an inference-time scaling approach that is independent of the number of inference steps. We propose a simple approach using best-of-$N$ scaling, following the procedure: sample actions independently and choose the best sample using a verifier. In our offline RL algorithm, we have a natural verifier: the $Q$-function. Thus, we can implement best-of-$N$ sampling as follows: given a state $x$, sample $a_1, a_2, \ldots, a_N$ independently from the policy $\pi_\theta(a \mid x)$ and select the action with the largest $Q$ value.
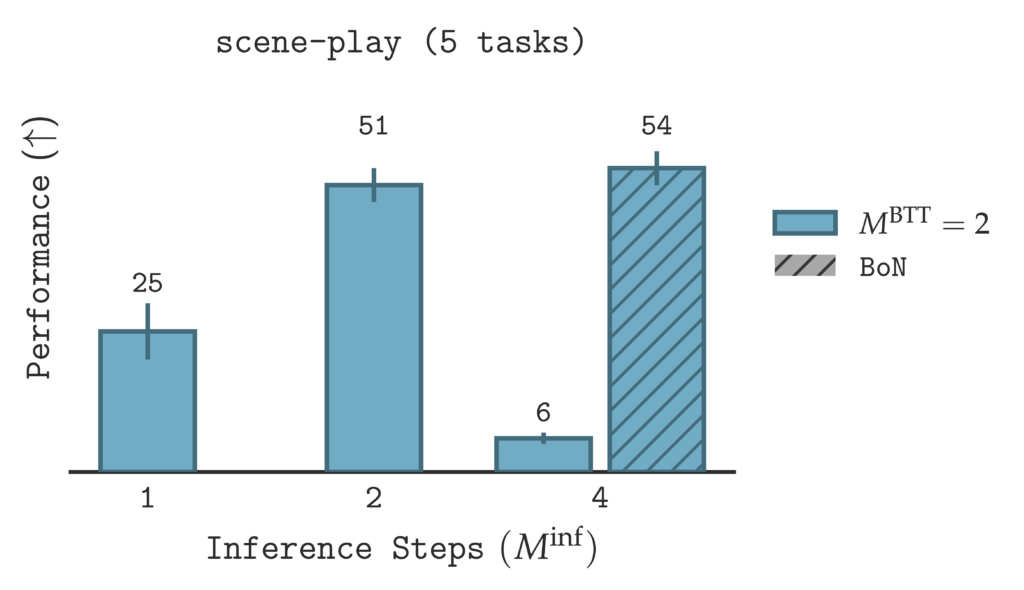
Notably, a common problem with LLM test-time scaling, such as chain-of-thought (CoT), is extrapolating beyond what was optimized during training. In other words, if $M^{\text{BTT}}$ steps were optimized with backpropagation through time, then inference typically has to use fewer steps (i.e., $M^{\text{inf}} \leq M^{\text{BTT}}$). We show that $\texttt{SORL}$ can do better, specifically:
$\texttt{SORL}$’s sequential and best-of-$N$ scaling enables sequential extrapolation: $\texttt{SORL}$ can use a greater number of inference steps at test time than the number of steps optimized during training.
Given a fixed training budget (i.e., a fixed number of backpropagation steps through time $M^{\text{BTT}}$), we evaluate on an increasing number of inference steps $M^{\text{inf}}$. Normally, when the number of inference steps is greater than the number of steps optimized during training (i.e., $M^{\text{inf}} > M^{\text{BTT}}$), the performance degrades significantly ($M^{\text{inf}}=4$). However, when sequential scaling is combined with best-of-$N$ sampling, denoted by the `/` striped bars in the figure above, $\texttt{SORL}$’s performance improves. Thus, $\texttt{SORL}$ can use more inference steps than the number of steps optimized during training, up to a performance saturation point.
Parting Thoughts
In this post, we explored how to scale offline RL along three key axes: data, model capacity, and test-time compute. While prior work has focused on scaling data and models, we showed that scaling inference-time computation is a promising avenue for improving offline RL performance.
At the core of our approach is the shortcut model: an expressive generative policy class that is uniquely suited to reinforcement learning. Unlike traditional diffusion or flow-based models, shortcut models allow for flexible sampling with a small, varying number of denoising steps, making them both expressive enough to model complex, multimodal behaviors and efficient enough for RL training.
We believe our work opens a promising direction for offline RL: rather than focusing solely on training-time improvements, we consider methods that benefit from inference-time scaling. One exciting avenue for future work is adaptive inference, where the number of sampling steps is dynamically determined (e.g., $Q$-function gradients).
For more details, check out our paper and codebase (links below).



