How Does Critical Batch Size Scale in Pre-training? (Decoupling Data and Model Size)

Pre-training large machine learning models is resource-intensive, involving a multitude of decisions around various factors such as model size, data selection, and optimization hyperparameters. These decisions carry high stakes, as each pre-training run can cost millions of dollars. However, experimenting directly at massive scale is rarely feasible.

Scaling laws offer a solution: they let us extrapolate from smaller-scale experiments, providing insights that guide decisions without the prohibitive costs. The well-known Chinchilla scaling law ($C \approx 6ND$) concretely balances compute budget with performance, helping us make informed trade-offs between model size (N) and dataset size (D). These laws help navigate the trade-offs between increasing N, D, and total compute C. However, they overlook critical factors such as wall clock time, which is essential for practical deployment. Wall-clock efficiency is heavily influenced by batch size, as data parallelism can significantly reduce runtime. This strategy is particularly emphasized in a recent blog post by EpochAI, which highlights that future model development may increasingly be constrained by communication latency. To address this “latency wall,” a practical approach is to scale up the batch size, as discussed in detail here. 

Understanding this trade-off brings us to the focus of this blog post, the concept of critical batch size, defining the point beyond which increasing the batch size no longer reduces wall-clock time without incurring additional compute overhead. Research by McCandlish et al. (2018) and Shallue et al. (2019) shows that below the critical batch size, training benefits from faster convergence with minimal additional cost, enabling more efficient use of resources. This makes understanding and optimizing batch size a crucial aspect of large-scale pre-training, especially when computing costs and runtime constraints are both critical considerations in planning multi-million-dollar training runs.

What is Critical Batch Size?

The notion of Critical Batch Size (CBS) arises from balancing the gains of data parallelism with diminishing efficiency returns as batch size increases. Linear scaling can occur in regimes where the batch size is below the CBS: doubling batch size proportionally halves the number of optimization steps required to reach a target loss (Dashed orange line), maintaining a direct, efficient relationship between batch size and training speed. However, beyond the CBS, this scaling no longer holds, and further increases in batch size do not significantly reduce the number of steps required.

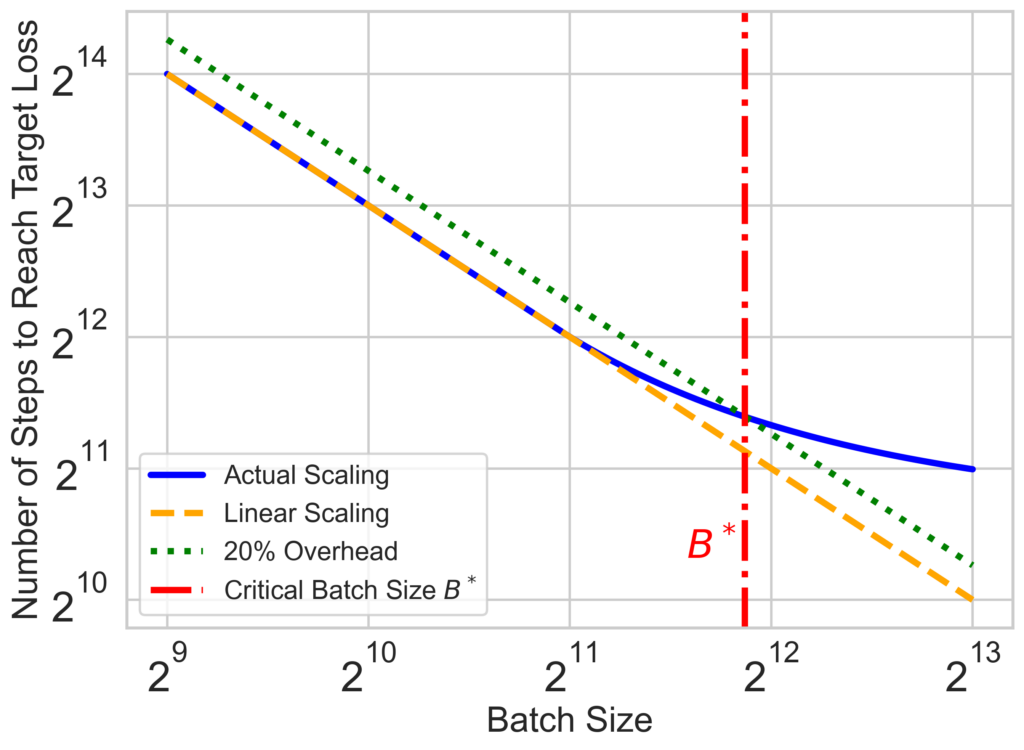
We formally define Critical Batch Size (CBS) B* as the batch size where the number of optimization steps required to reach a target loss increases by 20% over the linear scaling regime. B_opt is the maximum batch size in the linear scaling regime. CBS essentially marks the point where further scaling does not result in significant gains in terms of computational steps saved. This is particularly important in the pre-training of large models, where hardware resources are often constrained.

Our Results

Empirical Findings

The study investigates the CBS in the context of autoregressive transformer-based language model pre-training, using models ranging from 85 million to 1.2 billion parameters, trained on the C4 corpora. Through a series of controlled experiments, several key findings emerge:

• Qualitative scaling of CBS: We observe that, in usual settings where model and data size are scaled proportionally, CBS increases as we scale up (left). When controlling for model size N, increasing data size D (middle) results in increases in CBS. However, when controlling for dataset size D (right), the CBS does not scale with model size. This suggests that the amount of data plays a more significant role in determining the CBS than the model size itself.

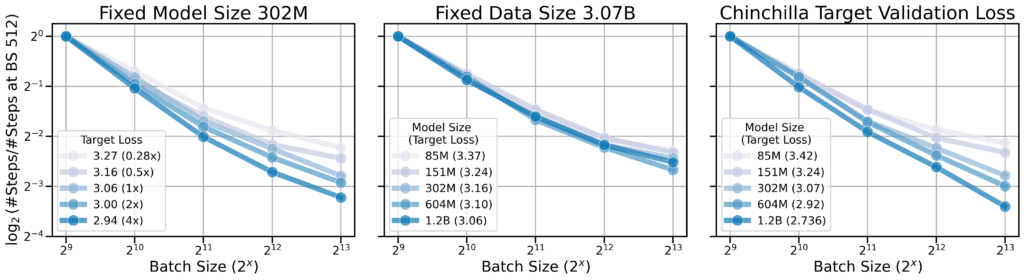
• Scaling Laws for CBS: We quantitatively study such relationships (plots below correspond to three settings above) and found that CBS scales with the size of the data (middle) according to a power law:

CBS ∝ D^0.47

where D is the dataset size, this indicates that (over-)training on more data for longer allows for more data parallelism and reduces the number of optimization steps needed to reach a target loss.

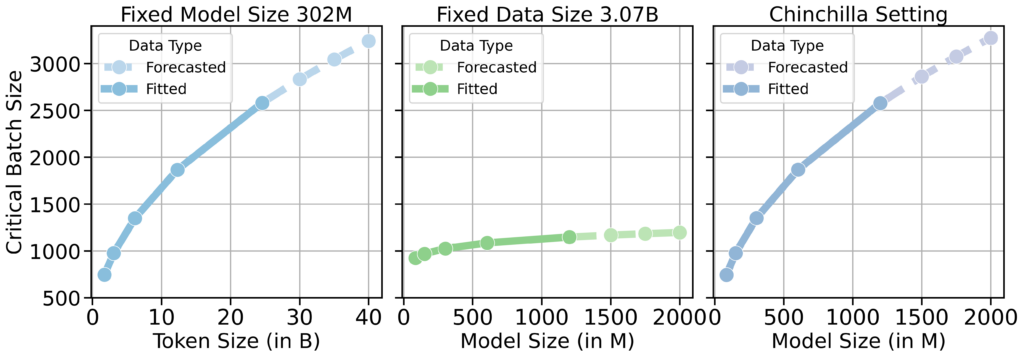
Overall, we found in experiments where the data size was held constant and only the model size was increased, CBS remained unchanged. Conversely, increasing the data size while keeping the model size fixed resulted in a proportional increase in CBS.

Theoretical Justifications

We also provide theoretical support to the empirical scaling observed for CBS with model and data size. 

1. Fixed data size, increasing model size: Theorem 1 demonstrates that in infinite-width regimes, for a fixed dataset size, training behavior becomes effectively independent of model size. This implies that for sufficiently large models, CBS remains constant, underscoring that expanding model size alone doesn’t demand proportionally larger batches.

Theorem 1 (Informal version of Theorem 2). In infinite width regimes (Yang and Hu, 2021), for a fixed dataset size, training dynamics and performance of the networks become effectively independent of the model size. Consequently, the critical batch size remains nearly invariant when scaling up the model size beyond this point, indicating that larger models do not require proportionally larger batch sizes to achieve optimal training efficiency.

2. Fixed model size, increasing data size: For mini-batch stochastic gradient descent (SGD) applied to least squares problem, under power-law assumptions on the spectrum, we theoretically show that CBS increases with dataset size $D$. 

Corollary 1 (Informal version of Corollary 2). Consider mini-batch SGD with D samples in the least square problems under power-law source and capacity conditions. The CBS, which enables mini-batch SGD to achieve the minimal expected excess risk while ensuring the fastest possible serial runtime, is given by $B^*(D)=\Theta\left(D^c\right)$, where the exponent $c \geq 0$ is determined by the exponents of the source and capacity conditions. In the regime where the variance error tends to be dominant, we have $0<c<1 / 2$, indicating CBS grows with data size.

Conclusion

The key takeaway is that CBS scales primarily with dataset size, not model size. For practitioners, this means that increasing batch sizes beyond the CBS does not yield significant efficiency gains and that focusing on dataset size is more beneficial for optimizing data parallelism. The findings may offer practical insights into efficient scaling strategies for pre-training large language models.