LOTION: Smoothing the Optimization  Landscape for Quantized Training

Large language models (LLMs) have ballooned in size because larger models consistently and predictably perform better on a wide range of downstream tasks. GPT-3, released in 2020 by OpenAI, had 175 billion parameters and was trained on roughly 500 billion tokens. In contrast, DeepSeek V3, released last winter, had 671 billion total parameters and was trained on around 14.8 trillion tokens – nearly a 4x increase in parameter count and a 30x increase in data budget in just 4 years!

The parameter counts and training budgets of other state-of-the-art foundation models are not public, but many of them are estimated to be even larger. Empirical scaling laws show that performance increases smoothly as a function of parameter count, training data size, and compute budget, yielding an attractive performance-compute tradeoff: by simply leveraging scale, you can usually buy dramatic increases in model capability.

However, scaling these models is a double-edged sword as deployment costs rise accordingly with parameter count. Larger models demand more memory bandwidth and FLOPs per token generated, driving up both serving costs for the model provider and response times for the end users. Given that the number of FLOPs spent serving a foundation model over its lifetime typically dwarfs the compute budget needed to train it, decreasing these inference costs is a pressing issue. Quantization and low-precision deployment are standard practices for reducing memory footprint and inference time, allowing us to continue exploiting scale for practical model performance.

Deploying precision and quantization

The numerical precision of a model refers to the number of bits allocated to represent each parameter or activation. Using high precision float formats like BF16/FP32 yields a more accurate representation of a given number but can lead to greater storage costs and longer computation times. For example, storing a 100B parameter model in FP32 would require 400GB (32 bits * 100 billion parameters) of memory for the weights alone. Autoregressively decoding tokens at inference time is typically bottlenecked by the cost of shuttling all of these parameters along the memory hierarchy on a GPU. 

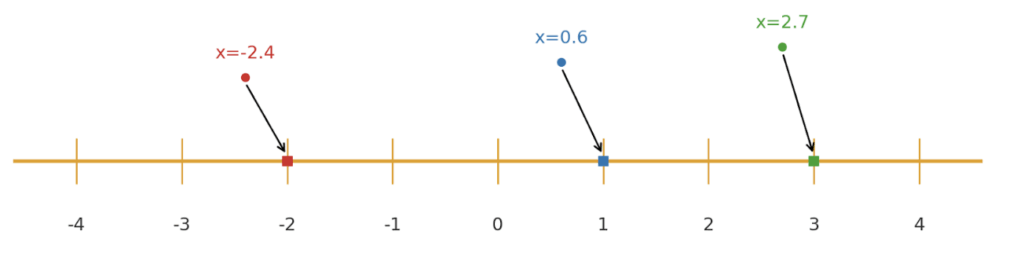
Quantization alleviates this issue by mapping these high-precision weights to low-precision formats: instead of using 32 bits per number, we might use 8 or even 4 bits. For a simple example, consider the numbers -2.4, 0.6, and 2.7. Assume that our quantization bin thresholds are integers between -4 and 4. Then our three numbers would be rounded to the nearest integers -2, 1, and 3 as shown in Figure 1 below.

However, naively reducing the number of bits introduces rounding errors into computations. These rounding errors may be minor for individual weights, but given the massive amount of iterative computations needed to decode one token, this loss in precision can greatly harm model performance. 

Post-Training Quantization (PTQ) and Quantization-Aware Training (QAT) methods optimize for quantized model performance in order to mitigate this loss in accuracy. PTQ methods typically pretrain in full precision and optimize simple surrogate objectives (e.g. layer- or matrix-multiply-specific reconstruction error) rather than retraining the full model. These methods are cheaper and faster but typically underperform QAT, particularly at lower bit-widths. Given the original objective L(w), QAT methods try to directly optimize the quantized objective L(Q(w)) where Q is the quantization operation that maps weights to a finite codebook of possible representations. Figure 2 depicts a simple 1-D quadratic loss and its quantized counterpart. 

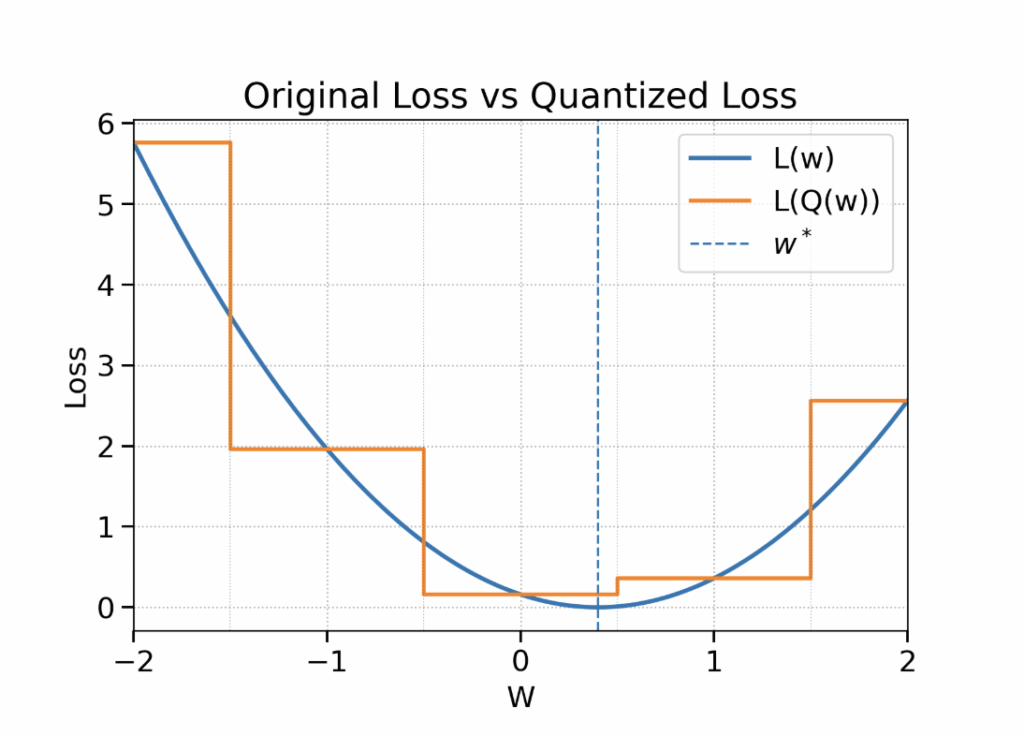
Unlike in this simple toy example, quantizing the minimizer of L(w) for complex, real-world models generally does not minimize L(Q(w)). QAT therefore targets the quantized objective directly. However, as shown in the figure, quantization renders the loss surface piece-wise constant, so the objective is non-differentiable: gradients are zero everywhere except at quantization thresholds where they are undefined. To optimize this objective, QAT must rely on the straight-through estimator (STE). QAT methods typically compute the gradient directly with respect to the quantized weight, treating the quantization operation as the identity (pretending $\frac{\partial Q}{\partial w} \approx 1$). Despite some empirical success, these naive STE-based methods are unprincipled and tend to become unstable at low bitwidths.

LOTION

In our paper, we introduce LOTION – Low-precision Optimization via sTochastic-noIse smOothiNg – a method that smooths the quantized loss, eliminating the need for the STE. Recall that the core problem with quantization is that it transforms a smooth loss landscape into a giant staircase, as shown in Figure 2. On the flat part of each step, the gradient is zero, and at the sharp edges, it’s undefined. An optimizer like SGD tries to walk down this staircase but has no local signal of where to go. QAT provides a gradient signal, but STE-based updates can be very brittle, particularly when the steps in the staircase are relatively large (e.g. in lower precision). Consider a point on the lowest step on the staircase. This point minimizes the quantized loss, but QAT may yield a gradient that can push us out of this step into a range where the quantized loss is higher.

LOTION solves this issue by computing the expected loss over the distribution of all possible randomized rounding outcomes. This averaging process replaces the staircase with a smoother “ramp.” On this new landscape, the gradient is well-defined almost everywhere, allowing any standard optimizer to follow the slope and descend towards a minimum. This smoothing procedure also provably preserves all the global minima of the original quantized problem, meaning that we are still optimizing for the best possible quantized network. The effect of LOTION is shown in Figure 3 below:

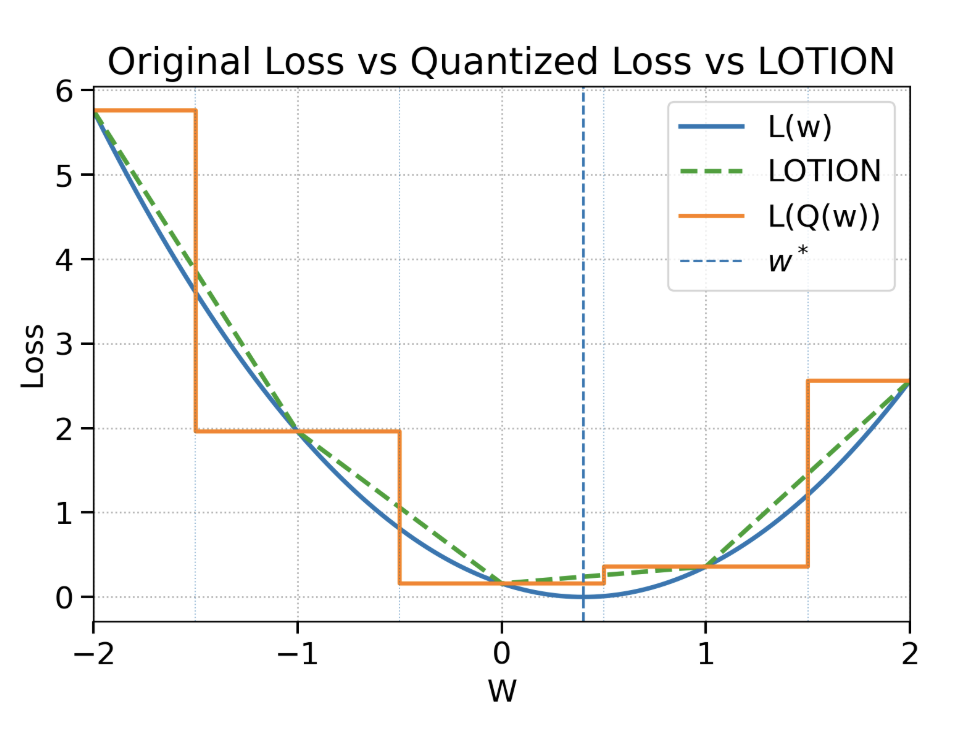
LOTION

We define the smoothed objective as follows:

\[
\mathcal{L}_{\textrm{smooth}}(w)
= \mathcal{L}(w)
+ \frac{1}{2} \textrm{tr} \left(H(w)\,\Sigma_\varepsilon(w)\right)
\],

where $H(w)$ is the Hessian matrix, and $\Sigma_\varepsilon$ is the covariance of randomized rounding noise.

Computing the full Hessian H(w) is impractical, so we use the Gauss-Newton/empirical Fisher approximation by accumulating the square of the gradients as we would in Adam. Although LOTION does not depend on a specific noise distribution, we choose to use stochastic rounding because it is practical, zero-mean, and closely mirrors the standard quantization operation.

The randomized-rounding operation rounds values up or down to the nearest quantization bins with probability proportional to the distance from each bin. Referring back to the quantization example, randomized rounding would individually round each of our values -2.4, 0.6, and 2.7 to their corresponding lower or upper integer thresholds with the probabilities shown below in Figure 4.

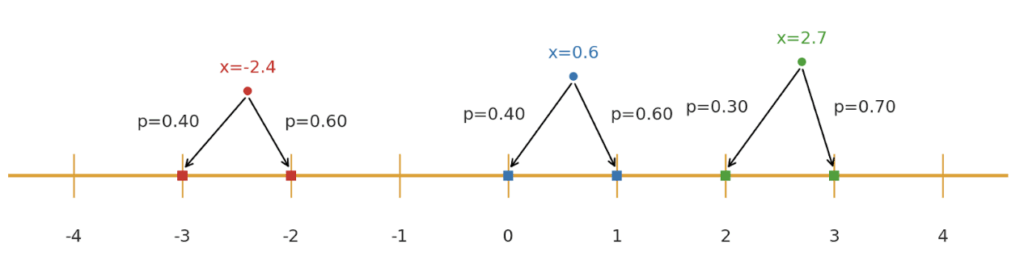
When stochastically rounding a block of parameters, we first scale the group into the range of values that are representable by the chosen precision format. Once we obtain this scale, we can easily compute a closed-form expression for the covariance of the randomized rounding. Because each parameter is rounded independently after scaling, we can compute this value for each parameter separately.

Language Model Experiments

We validate LOTION’s performance on 150M- and 300M- parameter language models against two baselines: 1. standard QAT with the STE and 2. direct quantization after training in full precision (PTQ). In our paper, we compare these methods at three different levels of precision: INT8, INT4, and FP4. 

When quantizing to INT8, weights are mapped to integers ranging from -127 to 127. The large number of quantization bins mitigates accuracy loss while allowing for speedups compared to 16- and 32-bit formats. INT4 quantization constricts values to integers between -7 and 7, halving the memory bandwidth compared to INT8 at the cost of greater accuracy loss. Tensor Core acceleration for both INT4 and INT8 are standard on many modern NVIDIA datacenter GPUs, including the Ampere A100. Although INT4 and INT8 are both integer formats with uniformly spaced quantization bins, weights and activations rarely follow this distribution. FP4 formats allow for the dynamic range advantages of floating point formats while maintaining the memory footprint of INT4 precision.

NVIDIA’s newest Blackwell chips offer hardware support for multiple variants of FP4 including MXFP4 and NVFP4 for high-throughput inference. OpenAI recently released its open-source GPT-OSS along with checkpoints quantized to MXFP4, enabling even the larger 120B parameter model to run on one GPU. Optimizing models for these new low-precision formats while maintaining fidelity to the full-precision model is crucial to maximizing inference throughput. As mentioned earlier, quantizing to these low-precision formats introduces rounding errors that may be minor for individual weights but quickly compound over the iterative text generation process. Even slight increases in loss can noticeably degrade model performance.

We demonstrate that LOTION preserves the validation loss of the full precision model compared to existing QAT methods for Large Language Models, particularly when quantizing to extreme bit-widths. We present a subset of results below. Figure 5 compares the quantized validation loss when quantizing a 150M parameter model using LOTION and standard QAT. We train this model on 15 billion tokens and find that LOTION continues to decrease the quantized validation loss while QAT plateaus. It is a commonly held belief that larger models are more robust to quantization. We question whether scaling up model size will eliminate the performance gap between LOTION and QAT. 

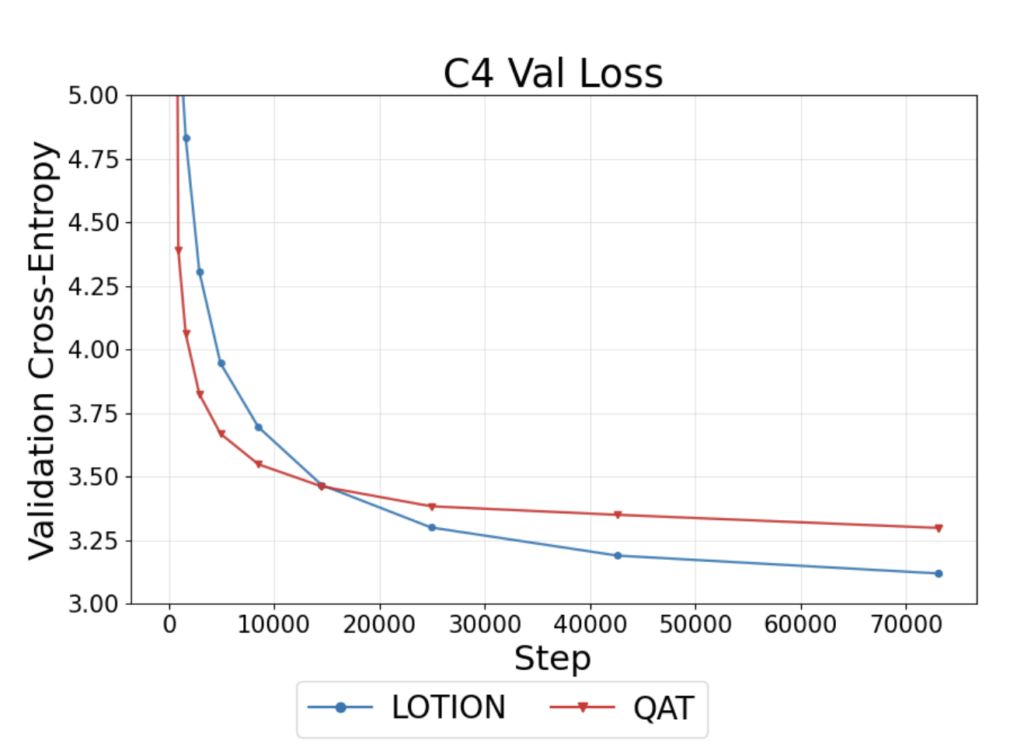
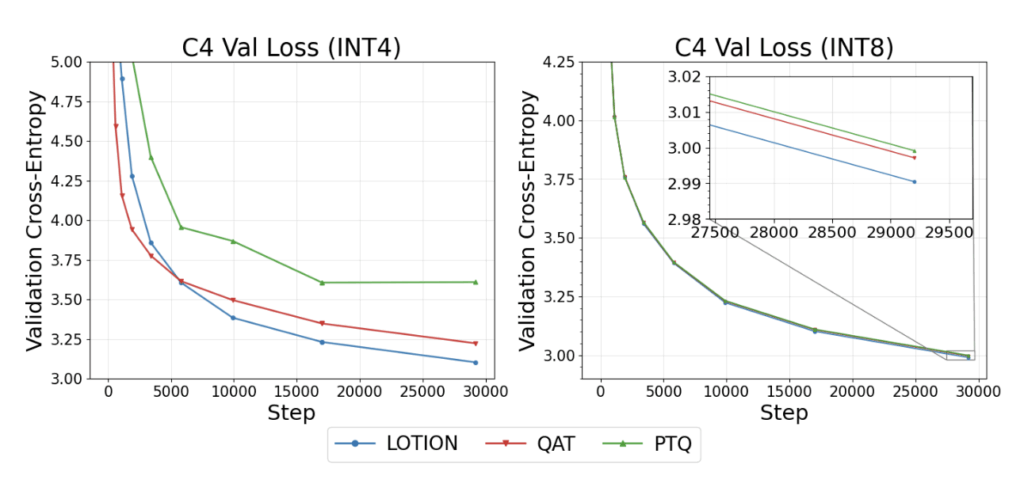
In Figure 6, we compare PTQ, QAT, and LOTION on a 300M parameter model. For both INT 8 and INT4 quantization, we find that LOTION outperforms both PTQ and QAT. PTQ performs the worst on the quantized validation loss, further supporting the claim that merely quantizing the minimizer of the original loss is insufficient to minimize the quantized loss. The differences in performance between these three methods are exacerbated at INT4 because the quantization error is larger with fewer bits allocated per number. Finally, quantization to modern precision formats like FP4 is generally favored over INT4 because of its non-uniform quantization scheme that can represent small values while accounting for rare large outliers. This increased resolution for values near zero tends to lead to lower overall quantization error and higher inference accuracy. We question whether these new precision formats will nullify any meaningful performance differences between the different quantization methods. 

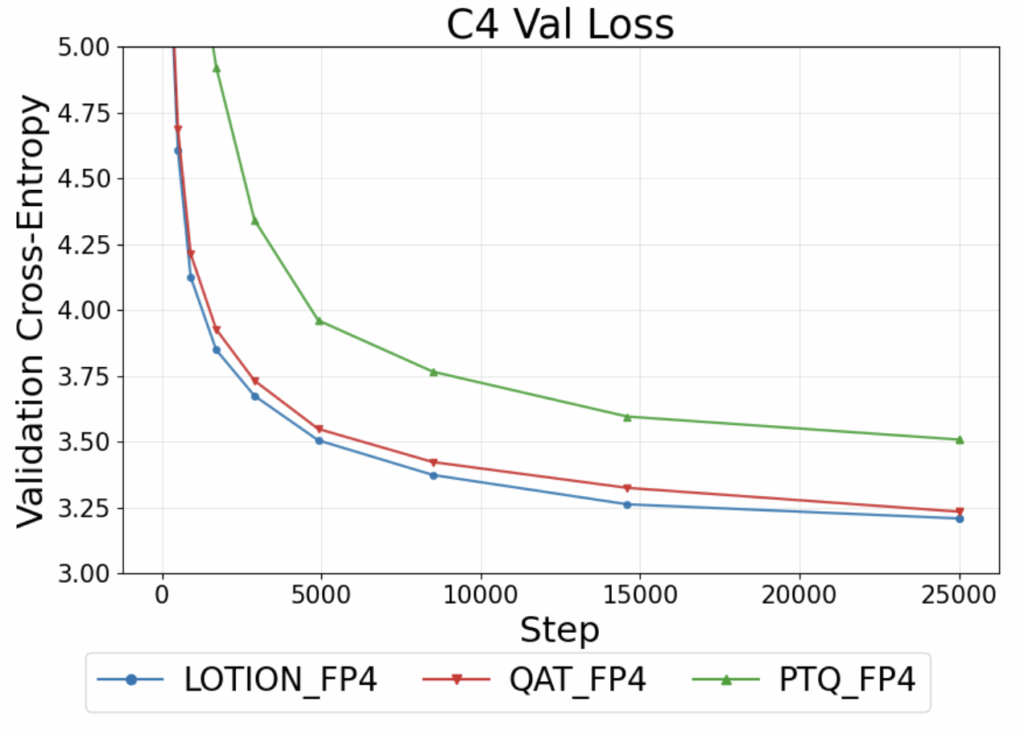
In Figure 7, we quantize a 150M parameter model to FP4. We find that LOTION continues to outperform both QAT and PTQ in this format.

Looking forward, we are excited to extend LOTION to different precision formats and noise distributions. One of the key strengths of LOTION is that it is an adaptable framework that can smooth different quantized loss functions regardless of the specifics of the quantization operation used. Furthermore, when using randomized rounding to smooth the loss surface, gradients are still nonexistent at quantization thresholds. Experimenting with different noise distributions to smooth the loss completely while preserving global minima is an interesting future direction of work.