Into the Rabbit Hull – Part I
November 12, 2025
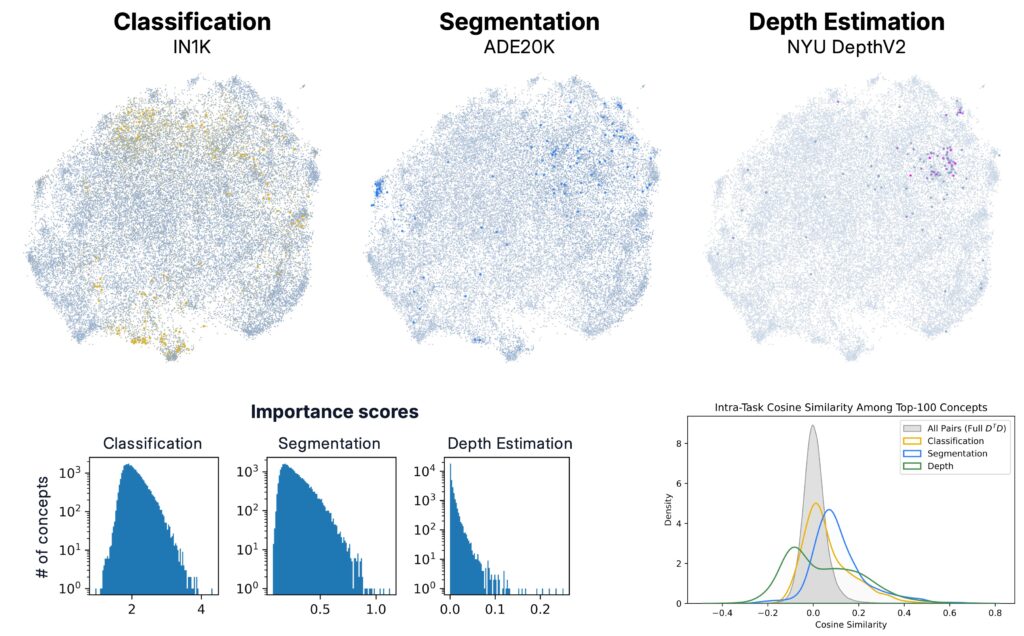
Overview of Part I: concept discovery in DINOv2 and task-specific organization across classification, segmentation, and depth estimation (top row).
This blog post offers an interpretability deep dive, examining the most important concepts emerging in one of today’s central vision foundation models, DINOv2.
This blogpost is the first of a two-part series based on our paper Into the Rabbit Hull: From Task-Relevant Concepts in DINO to Minkowski Geometry. In this work, we first examine — using current phenomenology — the most important concepts emerging in one of today’s central vision foundation models, DINOv2. We expose and study these concepts in detail before, in Part II, questioning the underlying assumptions that guide our interpretability methods. Finally, we synthesize our findings into a refined view of representational phenomenology inspired by Gärdenfors’ theory of conceptual spaces — the Minkowski Representation Hypothesis.
This first part is devoted to the finding using the current phenomenology, namely the Linear Representation Hypothesis.
Explore the interactive demo
DinoVision
Vision Transformers & DINOv2
Vision Transformers (ViTs) have redefined the foundations of visual representation learning. Inspired by the success of Transformer architectures in language, ViTs discard the convolutional inductive bias in favor of a more general, token-based framework: images are partitioned into fixed-size patches, each linearly projected into an embedding vector (a patch token), then processed by layers of self-attention and feedforward modules. This design unlocks a new regime of scalability and flexibility — and obeys more favorable scaling laws than convolutional networks.
DINOv2 is a paradigmatic example. Trained in a fully self-supervised manner on a massive corpus of unlabeled images, it has become a showcase of emergent visual representations.
Its embeddings support a remarkable variety of downstream tasks: fine-grained classification, segmentation, monocular depth estimation, object tracking, and even robotic perception. More impressively, DINOv2 features are now routinely used as priors in generative models and as proxies for distributional similarity across domains.
They are not only visually rich but also robust: DINO-based video models can predict physical dynamics from frames, and its embeddings can be aligned with language to achieve open-vocabulary segmentation and zero-shot classification — all without any textual supervision.
Yet despite these successes, the nature of DINOv2’s internal representations remains unclear. What, precisely, is encoded? Which features are available to downstream tasks, and how are they geometrically organized? More fundamentally, how can a label-free objective give rise to such effective, few-shot readout?
The Linear Representation Phenomenology
To address these questions, we turn to vision explainability, a field that provides both empirical tools and theoretical accounts for probing large vision models. A recurring observation is that their representational capacity far exceeds their number of neurons: in a d-dimensional space, networks can encode exponentially many features by representing each as a sparse linear combination of neurons.Empirically, these features behave as nearly orthogonal directions active in limited contexts, while neurons themselves are polysemantic, responding to multiple unrelated patterns.
This motivates two key ideas: (i) neurons are not the natural unit of interpretability, and (ii) one must instead recover the latent basis along which the model operates.
In other words, interpretability becomes a geometric problem — understanding how features are arranged within the activation space.
Early theoretical work proposed that this organization follows a linear and distributed scheme — often described as the Linear Representation Hypothesis (LRH). This hypothesis can be understood as a natural consequence of compression and coherence minimization: arranging features to minimize interference while maximizing retrievability.
Similar structures emerge across several scientific domains. In biology, the Dutch botanist Tammes (1930) studied how pores on pollen grains distribute over the spherical surface, finding that they repel each other to form maximally separated configurations — a pattern now known as the Tammes problem. In physics, an almost identical phenomenon appears in the Thomson problem, where identical electric charges constrained to a sphere settle into evenly spaced arrangements that minimize electrostatic energy. And in signal processing, the same geometry arises in the design of spherical codes, which aim to place codewords (or basis vectors) as far apart as possible on the hypersphere to minimize interference between signals.
This common mathematical substrate — formalized as Grassmannian frames — provides the a idealized case of the Linear Representation Hypothesis, the idea that deep networks may implicitly approximate such optimal configurations when organizing their internal features.

This pervasive pattern makes it a compelling hypothesis for how deep networks might implicitly organize their internal representations: maximizing the number of retrievable features while minimizing interference between them. Formally, the LRH could be defined as follows:
Definition — Linear Representation Hypothesis (LRH)
A representation $\mathbf{a} \in \mathbb{R}^{d}$ satisfies the linear representation hypothesis if there exists a sparsity constant $k$,
an overcomplete dictionary $\mathbf{D} = (\mathbf{d}_{1}, \dots, \mathbf{d}_{c}) \in \mathbb{R}^{c\times d}$,
and a coefficient vector $\mathbf{z} \in \mathbb{R}^{c}$ such that $\mathbf{a} = \mathbf{z}\mathbf{D}$, under the following conditions:
\begin{cases}
(\mathbf{i})\text{ Overcompleteness:} & c \gg d, \\[4pt]
(\mathbf{ii})\text{ Quasi-orthogonality:} &
\mu(\mathbf{D}) \equiv \max_{i\neq j}|\mathbf{D}_{i}\mathbf{D}_{j}^\top| \le \varepsilon,\quad \|\mathbf{D}_{i}\|_{2}=1, \\[6pt]
(\mathbf{iii})\text{ Sparsity:} & |\operatorname{supp}(\mathbf{z})| \le k \ll c.
\end{cases}
The LRH is useful precisely because it can be operationalized!
If activations indeed admit such a sparse, overcomplete representation, then concept discovery reduces to dictionary learning: recovering the basis vectors along which the model represents information.
Classical approaches to dictionary learning include Non-negative Matrix Factorization (NMF), Sparse Coding, and, more recently, Sparse Autoencoders (SAEs) — efficient, large-scale instantiations of the LRH that provide practical access to the latent basis. In our study, we adopt an Archetypal Sparse Autoencoder (SAE), a stable variant that constrains each dictionary atom to lie in the convex hull of real activations (see: Archetypal SAE, Fel et al., ICML 2025).
Given a set of activations $A$, the SAE learns a code matrix $Z$ and a concept basis $D$ such that:
\begin{align}
A = ZD, ~\text{with}~ Z \geq 0, ||Z||_0 \leq k ~\text{and}~ D \in \text{conv}(A)
\end{align}
Interpreting $Z$ and $D$
Essentially, the matrix $Z$ encodes the statistical structure of the activation space — which concepts are active, how frequently, and to what degree. The dictionary $D$, in contrast, encodes the geometric structure — the atomic directions that span the space and organize DINOv2’s internal feature basis.This decomposition yields a library of 32,000 concept atoms, each interpretable as a linear probe on DINOv2 activations.
With this foundation in hand, we can ask: Which concepts are recruited by different downstream tasks? And how are these concepts geometrically and statistically organized?
These questions mark the beginning of our descent — the first step into the Rabbit Hull.
Task-Specific Utilization of Concepts
With the concept dictionary in place, we now ask a natural question: which of these concepts are actually used across downstream tasks?
To address this, we examine how task-specific linear probes interact with the concept dictionary — effectively measuring how each downstream objective projects onto the learned basis.
We focus on three central vision tasks, two of which involve dense prediction: classification, segmentation, and monocular depth estimation.
These three represent complementary perceptual goals — from object identity to spatial layout and geometric inference — and thus provide a structured way to probe functional specialization within DINOv2.
Different Tasks Recruit Different Concepts
When measuring concept alignment across tasks, we find that different tasks recruit distinct regions of the concept dictionary, often with minimal overlap.
- Classification engages a broad and dispersed set of concepts spanning much of the dictionary.
- Segmentation and Depth Estimation instead rely on more compact, geometrically coherent subsets.
This asymmetry indicates that DINOv2’s internal representations are functionally organized: some families of concepts are selectively reused for specific perceptual computations.
Quantitatively, classification draws from a larger fraction of the dictionary, consistent with its higher output rank and categorical diversity, whereas dense prediction tasks activate narrower, low-dimensional subspaces.
Classification — Elsewhere Concepts
In the context of classification, we observe a consistent and interpretable pattern. For each ImageNet class, two dominant concepts tend to emerge:one that activates on the object itself (e.g., “rabbit”), and another that activates everywhere else except the object, though only when the object is present. We refer to these as Elsewhere Concepts (following a suggestion by David Bau).

Elsewhere concepts exhibit a conditional structure: they respond to regions disjoint from the object, yet their activation depends on the object’s presence elsewhere in the image. They are not simple background detectors, but rather encode a relational property of the form: “not the object, but the object exists.”
This mechanism implicitly implements a form of spatial negation or distributed evidence representation.
From a computational perspective, such concepts can increase robustness: by distributing class-related evidence across both object and contextual regions, DINOv2 maintains stability under occlusion and spatial perturbations.
At the same time, they expose a limitation of standard interpretability tools — activation-map visualizations can be misleading, as the spatial regions of maximal activation are not necessarily the regions causally responsible for that activation, particularly for transformers where long-range information transmission is pervasive. In other words, those features violates the unspoken assumption of heatmaps visualization: The concept is just about the token where the concept fires.
This highlights the need for interpretability tools that take both concept localization and causal perturbation into consideration. Having explored classification, we now turn to the task of semantic segmentation.
Segmentation — Boundary Concepts
When analyzing segmentation, we find that the most important concepts localize sharply along object contours — highlighting boundaries, edges, and silhouette transitions.
Across categories, these boundary concepts show highly consistent spatial footprints: they fire at the periphery of objects, whether biological (e.g., limbs, heads) or architectural (e.g., rooflines, domes).

That suggest that DINO allocates a dedicated region of its representational space to encoding object boundaries. As quantitatively shown in the paper, the absolute cosine similarity of those concepts is higher than average and their eigenspectrum decays faster than a random subset of concepts suggesting a low-dimensional structure composed of boundary detectors.
Segmentation concepts reveal that DINO dedicates portions of its concept space to encoding local spatial structure. We now examine depth estimation, another spatially grounded task, but one that requires global 3D understanding rather than local contour localization.
Depth Estimation — Monocular Cue Concepts
For depth estimation, the story differs again.
Although DINOv2 is trained without explicit 3D supervision, its internal features support accurate monocular depth predictions.
By perturbing and analyzing depth-relevant concepts, we identify three principal families of features corresponding to canonical monocular cues:
- Projective geometry cues — sensitivity to perspective lines and structural convergence.
- Shadow-based cues — sensitivity to soft lighting gradients and cast shadows.
- Texture-gradient cues — sensitivity to changes in spatial frequency, analogous to blurring or photographic bokeh.
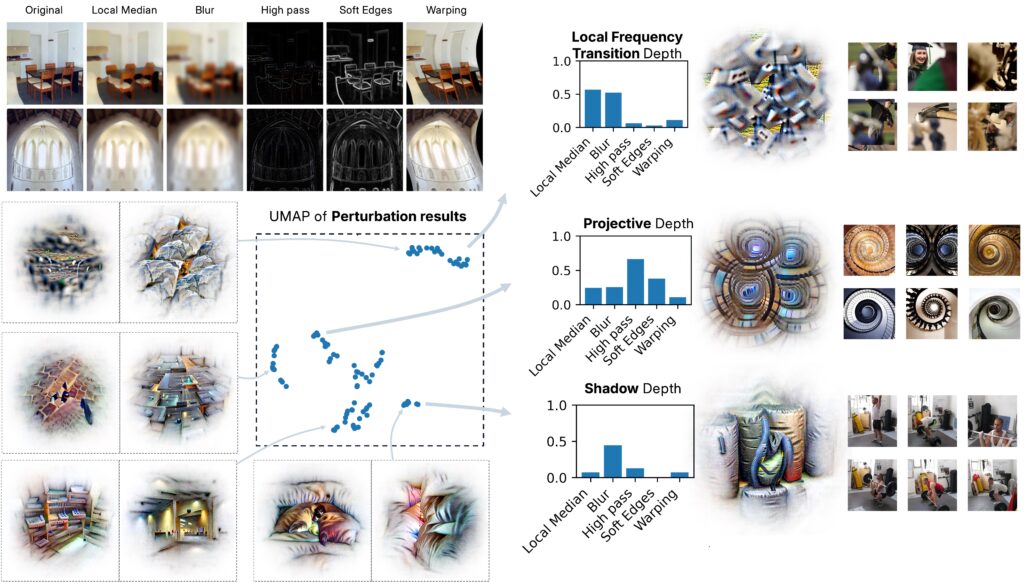
Most concepts show mixed sensitivity across these cue types, but a subset remains strongly selective. Together, these clusters define a well-structured subspace within the concept dictionary. This organization mirrors findings from human and animal vision, where similar cue families underlie depth perception.
Hence, even in the absence of geometric supervision, DINOv2 spontaneously acquires interpretable 3D perception primitives from 2D input statistics — an instance of emergent perceptual structure within a purely self-supervised model.
Register Tokens — Global Scene Concepts
So far, we have examined DINO concepts primarily through the lens of semantic content and task alignment. However, Vision Transformers possess a structural dimension that standard interpretability often overlooks: the diversity of token types.
Not all tokens serve the same role. In DINOv2 and related ViT architectures, spatial tokens correspond to image patches, while cls and register tokens are explicitly designed for global processing — aggregating scene-level or inter-token information.
This architectural asymmetry raises a natural question: are some concepts specialized for specific token types, and do they occupy distinct subspaces within the concept geometry?
To investigate this, we analyze the footprint of each concept — the distribution of its activations across token positions. Concepts with low footprint entropy activate consistently on specific token subsets, indicating positional or token-type specialization, whereas high-entropy concepts are spatially diffuse and token-agnostic.
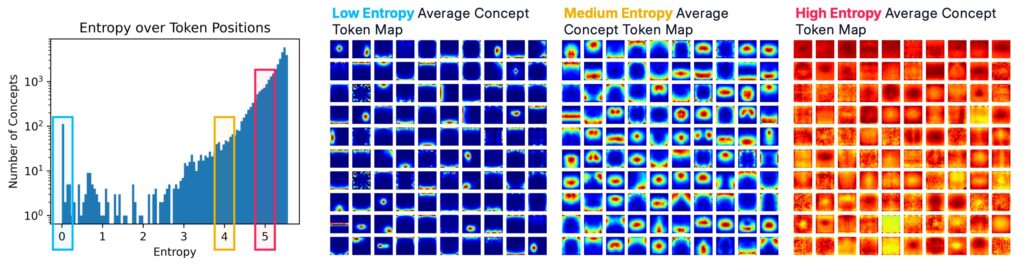
When inspecting these specialized concepts, a clear pattern emerges. A large group of concepts activate exclusively on the register tokens, while almost none are exclusive to the cls token. This asymmetry is remarkable: only a single concept systematically fires on cls, but hundreds specialize for register tokens.

These register-only concepts differ qualitatively from patch-based ones. They do not correspond to localized objects or regions but rather encode global, non-local properties of the image — such as illumination, motion blur, caustic reflections, artistic style, or even camera-level distortions like wide-angle warping or depth-of-field effects. They act as integrative features that summarize the overall “style” or “condition” of the scene, rather than its spatial composition.
This division of labor — a single cls-specific concept versus many register-specific ones — suggests that DINOv2’s internal architecture distributes high-level, abstract information across structurally distinct token pathways. Spatial tokens handle local, object-centric content, while registers encode global scene invariants, bridging the gap between perceptual structure and contextual regularities.
Summary
In this first part, we have applied the current working hypothesis of interpretability — the Linear Representation Hypothesis (LRH) — and its practical instantiation through Sparse Autoencoders (SAEs) to study the internal representations of DINOv2.
Using this framework, we discovered a large-scale dictionary of 32,000 concepts, each interpretable as a linear feature within the model’s activation space.
By analyzing how these concepts are recruited across downstream tasks, we found clear signs of functional specialization.
Different tasks rely on different subsets of the dictionary:
- Classification recruits distributed and relational features, including the Elsewhere Concepts, which activate in regions excluding the object but only when it is present — implementing a form of learned negation.
- Segmentation depends on Boundary Concepts, which localize precisely along object contours and form coherent low-dimensional subspaces.
- Depth Estimation draws on interpretable Monocular Cue Concepts — detectors for projective geometry, shadows, and texture gradients, resembling classical depth cues from human vision.
- In addition, we identified token-specific concepts, most notably register-only concepts encoding global scene properties such as illumination, motion blur, or style — revealing a structural division between spatial and global processing pathways.
In the next part, we will examine the geometry and statistics of the learned concepts more closely, and synthesize our finding in a refined view of representation as convex composition: the Minkowski Representation Hypothesis.



