Archetypal SAEs: Adaptive and Stable Dictionary Learning for Concept Extraction in Large Vision Models
March 20, 2025In recent years, the field of interpretability has focused heavily on concept-based approaches. As deep learning models advance to unprecedented scales in vision, language, and multimodal domains, the ability to automatically decompose learned representations into meaningful “concepts” has become one of the most promising interpretability strategies. Concept extraction attempts to identify semantically coherent, human-understandable directions or features within a neural network’s internal activations, giving us insight into what these high-dimensional representations encode.
Sparse Autoencoders (SAEs) have emerged as a powerful tool in this space, primarily because they can be trained similarly to standard neural networks and can scale to enormous datasets. Despite their promise, SAEs can exhibit a troubling phenomenon: instability. Two identical SAEs trained on the same dataset (or even slightly perturbed versions of that dataset) can yield dictionaries that diverge wildly. This makes them unreliable for real-world interpretability needs or for dependable scientific applications.
Concept Extraction as Dictionary Learning
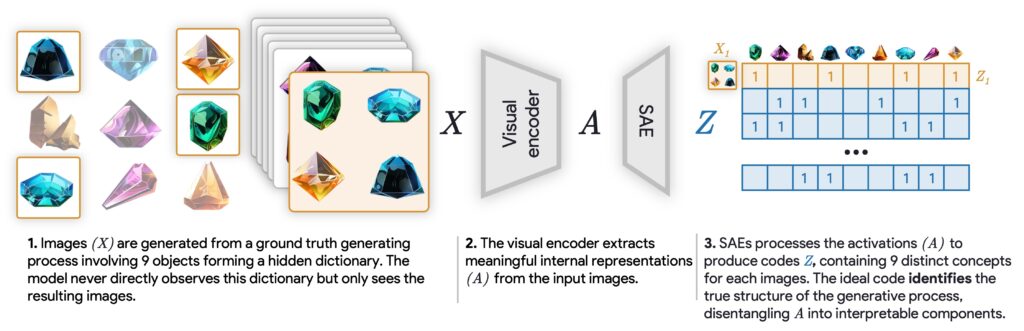
Our new paper first clarifies how each concept extraction method can be considered a particular instance of dictionary learning, where the data matrix consists of the deep model’s activations, and the dictionary is a set of learned concept directions. Formally, given a set of n data points in a d-dimensional feature space, represented as a matrix A, concept extraction aims to learn a dictionary D and codes Z such that:
$$
(Z^\star, D^\star) = \arg\min_{Z,D} ||A – ZD^T||_F^2
$$
The crucial objective is that these codes be suitably constrained, for example by sparsity or nonnegativity, which is believed to encourage interpretability.
In fact, most approaches that have been used are well-known dictionary learning approaches such that Nonnegative Matrix Factorization (NMF), K-means clustering, and principal component analysis (PCA).
\[
(Z^\star, D^\star) = \underset{Z,D}{\text{arg min}} \quad || A – Z D^T ||^2_F
\]
\[
\text{s.t.} \quad
\begin{cases}
\forall i,\, Z_i \in \{e_1, \dots, e_k \}, & \text{(ACE – K-Means)} \\[8pt]
D^T D = I, & \text{(PCA)} \\[8pt]
Z \geq 0,\, D \geq 0, & \text{(CRAFT – NMF)} \\[8pt]
Z = \Psi_{\theta}(A),\, ||Z||_0 \leq K, & \text{(SAEs)}
\end{cases}
\]
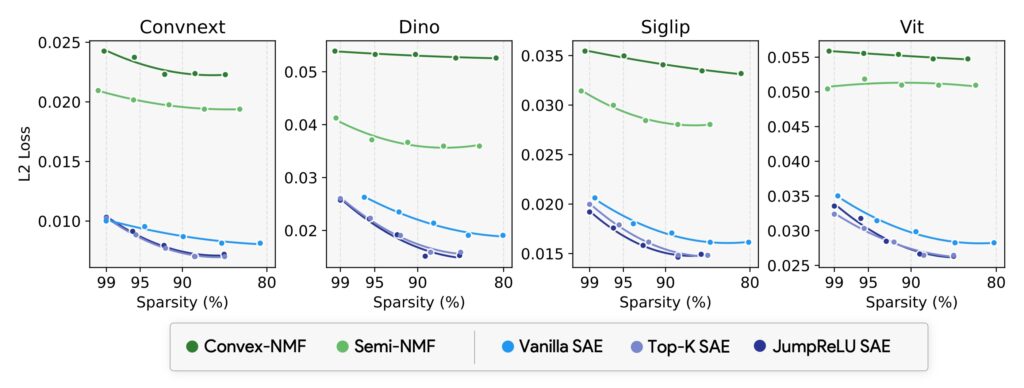
These approaches can be interpreted as variants of the same fundamental problem: learning a decomposition of the data into a set of vectors and sparse (or structured) codes. The advantage of SAEs over these older methods is that SAEs can scale up to modern data sizes by leveraging standard backpropagation and GPU-based optimizations. Specifically, a standard SAE trains a neural encoder-decoder structure, with the encoder producing sparse codes and the decoder’s weight matrix acting as the dictionary. However, as we find, this unconstrained approach often yields “floating” directions in the high-dimensional space, which are highly sensitive to small training perturbations.
(In)Stability of SAE
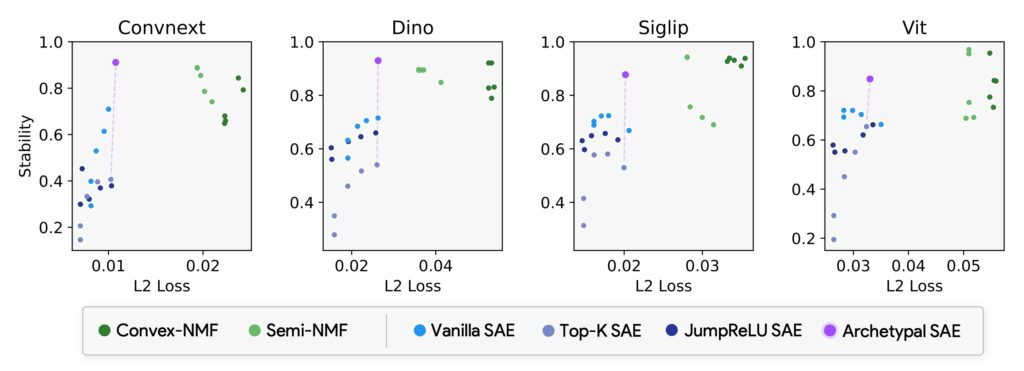
To investigate this instability, we propose a measure that quantifies whether two learned dictionaries end up close to one another. In our analysis, we define a stability score based on the optimal average cosine similarity. For two dictionaries D and D’, each holding a number of learned concepts, we look for the best one-to-one matching of concept vectors across the two runs and then compute the average cosine similarity. This can be written as:
$$
\text{Stability}(D,D’) = \max_{\Pi \in P(n)} \frac{1}{n} \text{Tr}(D^T \Pi D’)
$$
where $P(n)$ is the set of signed permutation matrices (or the set of all ways to match each dictionary atom in one model to an atom in the other), and $\text{Tr}(.)$ denotes the trace operator. If $D$ and $D’$ are very similar, their stability score will be closer to 1. In practice, the paper shows that popular SAEs often have a stability near 0.4 or 0.5, meaning that training your SAE on Monday, and retraining it on Tuesday replaces almost half of the learned concepts with completely different ones. This is obviously problematic for an interpretability pipeline, especially if we hope to trust or re-use the extracted concepts in further analyses.
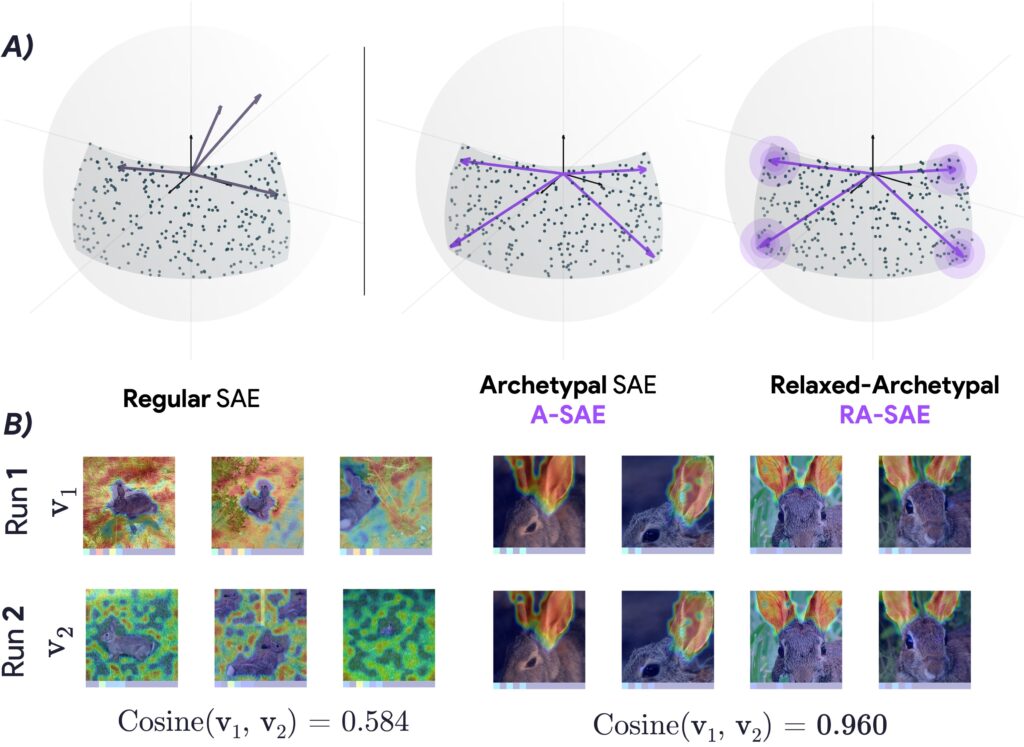
Archetypal SAE
Our central contribution is Archetypal SAE (A-SAE), which borrows the geometric anchoring principle from Archetypal Analysis, a method first introduced by Cutler and Breiman in the 1990s. The motivating idea is the constraint that each dictionary atom must live inside the convex hull of the data. This geometric restriction is extremely consequential. Because each concept vector or “atom” is forced to be a convex combination of real data points, that atom can no longer float off arbitrarily into the embedding space. As a result, the learned dictionary becomes far more stable, while still maintaining good reconstruction performance. The formal definition of the archetypal dictionary is as follows:
$$
D = W A \quad \text{s.t.} \quad W \in \Omega_{k,n}
$$
where $A$ is the entire dataset or some carefully selected subset, and $W$ is a row-stochastic matrix, meaning that each row of $W$ belongs to the $(n-1)$-dimensional simplex. Put differently, each dictionary atom (row of $D$) must be a convex combination of the data samples in $A$. At first glance, this approach might seem infeasible for large $n$, because storing a matrix $W$ with size $k \times n$ can be huge, and also because enumerating or mixing all possible points in the convex hull can be computationally expensive. We propose to tackle this by choosing a smaller set of anchor points or centroids, denoted by $C$, which is typically obtained by performing K-means on the data. If we let $C$ be those centroids, we then have:
$$
D = W C \quad \text{s.t.} \quad W \in \Omega_{k,n’}
$$
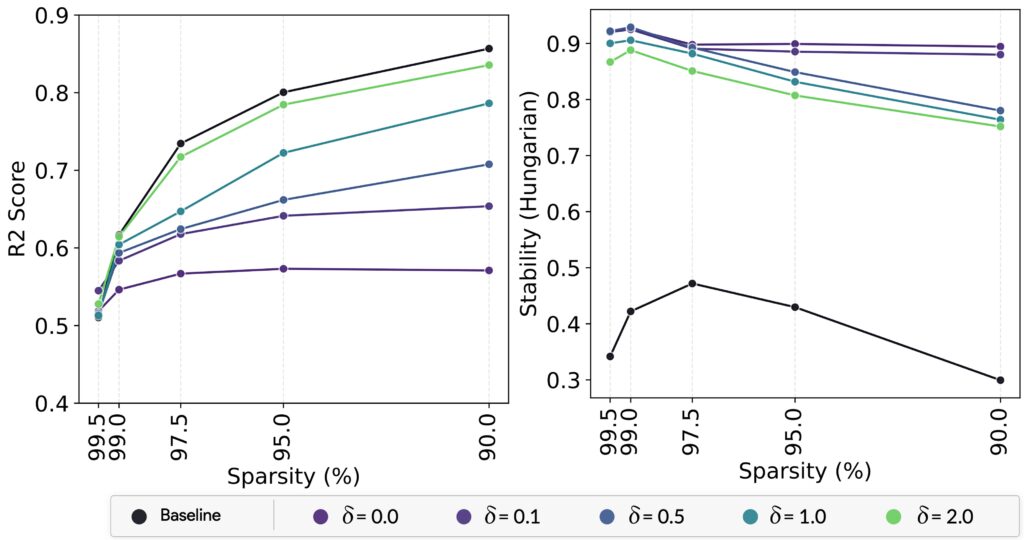
where $n’ << n$. This is computationally more tractable, and even though we lose some representational coverage by not using every single data point, we find that it makes A-SAE extremely stable across runs. The next refinement introduced is RA-SAE, or Relaxed Archetypal SAE, which allows for a small deviation outside the convex hull. In other words, while A-SAE enforces each atom to be exactly in convex hull of C, RA-SAE introduces a trainable shift matrix $\Lambda$ with a norm constraint: $$ D = W C + \Lambda, \quad \text{subject to} \quad \|\Lambda\|_2^2 \leq \delta $$ where $\delta$ is a small positive parameter. This modification is shown to improve expressivity by letting some dictionary atoms adjust slightly beyond the convex boundary if it helps reduce reconstruction error, all the while preserving most of the stability advantages. We show that even a small relaxation can bring the reconstruction error on par with unconstrained SAEs, and yet the dictionary remains near the real data manifold, preserving the improved stability.
Validation of Archetypal SAE
The paper includes thorough experiments with several well-known vision models, including DINOv2, ConvNeXt, ViT, SigLIP, and ResNet. We train both standard (unconstrained) SAEs and the proposed A-SAE or RA-SAE under identical conditions, with extremely large numbers of tokens (on the order of hundreds of millions of tokens). We measure a variety of metrics beyond standard reconstruction error and sparsity. One critical measure is an “OOD Score,” assessing how close each learned concept vector is to actual data points, and the “stability” metric described earlier. Another intriguing measure is how well the resulting dictionary lines up with an external classification head’s directions, that we call “Plausibility.” If each class’s final linear classifier weight vector can find a near-match among the dictionary atoms, that suggests the learned concepts are truly capturing directions that the model uses for recognition (and that probing the SAE concept will have an impact on the underlying model). RA-SAE emerges as the clear winner in terms of simultaneously maximizing stability, plausibility, interpretability, and reconstruction quality.
A highlight of the paper is the introduction of two novel benchmarks for evaluating dictionary learning in interpretability tasks. The first is a synthetic mixture benchmark, which we refer to as a “Soft Identifiability Benchmark.” We take a set of objects or classes that are composited into single images (like a collage of four different synthetic objects), run them through the network, and see if the dictionary learning approach can disentangle the underlying generative factors. In other words, can each “true” concept from the data generation pipeline reappear in the dictionary or in the learned codes. Standard SAEs do a decent job, but they often fuse different objects or fail to isolate them. In contrast, RA-SAE sees a consistent boost in accuracy, showing its ability to ground each dictionary atom in an actual concept from the data distribution.
The second benchmark is the plausibility test that checks alignment with classification directions. Specifically, for each class weight vector is paired with the closest concepts found by the SAE in the final layer, we then compute how aligned those pair are and average over all classes. This yields a measure of how well the dictionary covers the classification subspace: If plausibility is high, the dictionary is capturing many of the real signals that the classifier is relying on, suggesting that these directions are more than just random features. Again, RA-SAE yields higher plausibility scores than unconstrained SAEs.
We finish by providing additional qualitative results on real image data using DINOv2 embeddings. We train RA-SAE with 32,000 concepts, each corresponding to a row in the dictionary. Then, for a test image, we visualize the tokens (or patches) that activate a given concept strongly. We discover not only high-level semantic concepts like object parts (e.g., dog fur, rabbit ears, or building facades), but also less obvious or more localized features like shadows of dogs, barbers (as distinct from the client at a barber shop), or subtle shading of petals. An intriguing observation is that RA-SAE organizes these concepts more systematically compared to an unconstrained TopK SAE. For example, RA-SAE might consistently devote separate concepts to rabbits’ ears, their faces, and their tails, whereas an unconstrained SAE might conflate several of these parts into one single direction.
Qualitative Findings

Beyond quantitative analyses, our qualitative exploration of concepts learned by the RA-SAE method on DINOv2 embeddings revealed several intriguing and semantically meaningful insights. RA-SAE consistently surfaced interpretable concepts that were notably stable across different training runs.
One compelling discovery was the identification of very specific visual concepts such as a context-dependent “barber” concept, exclusively activating for the barber figure but not for their clients. Similarly, RA-SAE revealed subtle visual patterns such as “dog shadows,” potentially indicating that the model leverages shadow information for tasks like depth reasoning or object delineation.
Additionally, the method systematically identified clusters of fine-grained and spatial-relational concepts. For instance, RA-SAE learned distinct and stable concept clusters corresponding to parts of animals (e.g., clearly differentiating rabbits’ ears, faces, and paws), in contrast to unconstrained SAEs which frequently conflated these features. Another fascinating discovery was the emergence of spatial-relational concepts such as “bottom of,” “left of,” and “right of,” highlighting RA-SAE’s capability to reflect the intrinsic relational structure learned by vision models. These insights could potentially explain and provide interpretive grounding for object-matching behaviors and spatial awareness demonstrated by large-scale models like DINOv2.


In summary, our qualitative analysis underscores RA-SAE’s capacity for producing stable, semantically coherent, and insightful representations, offering a valuable lens through which researchers can reliably probe the rich internal structures of current large vision models.
Conclusion
In this paper, we offer an in-depth explanation of how standard SAEs, despite their scalability and good reconstruction performance, suffer from significant instability that can limit their practical interpretability. By introducing the idea of Archetypal and Relaxed Archetypal SAEs, we provide a simple yet highly effective geometric constraint: dictionary atoms must lie within or near the convex hull of the data. We demonstrate both theoretically and empirically that this constraint yields improvements in stability, plausibility, and semantic alignment with “true” concepts, including real classification directions. The framework, validated through new benchmarks and metrics, lays the groundwork for building more trustworthy, consistent, and meaningful concept-based interpretations in large vision models and beyond. It underscores a powerful lesson in interpretability: anchoring interpretations directly in real data is often the key to making them more reliable and transparent.



