Distinguishing the Knowable from the Unknowable with Language Models

Large language models (LLMs) are known to hallucinate. When generating text, models may (and often do) make assertions that are not correct. Of course, humans sometimes have the same tendency.^{[citation needed]} What makes the problem particularly pernicious is that LLMs tend to convey falsehoods with the same confident phrasing that they use to convey correct statements. This tendency severely limits the usefulness of LLMs—it is risky to trust them in high-stakes applications without verification of all of their outputs. Humans, on the other hand, seem to be capable of communicating in an uncertainty-aware way: we have a sense (albeit often a biased one) of how unsure we are of our claims, and if we are being responsible, we decide whether to say them, and how to say them, accordingly.

How can we endow LLMs with this metacognitive capability? A starting point is to use the probability values LLMs place on all the tokens they produce. In a pre-trained model, these reflect the model’s uncertainty about whether any given token would be the correct one if it encountered the preceding text during training. Empirical studies have found that (at least before the model is fine-tuned) these probabilities are well-calibrated in multiple choice question-answering settings: among cases where the model places a 30% probability that the answer is A, the answer is indeed A around 30% of the time.

This suggests a band-aid solution for hallucinations: simply display to the user the probabilities of every token in the model’s output, or highlight the low-probability ones. When the probability is low, this means the model has low confidence in the token. Suppose a model says “Vänern is the largest lake in the country of Finland”, but you see that it only places a 5% probability on “Finland”. This is a red flag that the model is hallucinating.

So is the band-aid solution sufficient? To see why not, suppose the model says “Sweden has beautiful lakes” and the probability on “lakes” is 5%. This does not mean the model “believes” there is only a 5% chance Sweden’s lakes are beautiful. Indeed, the remaining 95% of the model’s probability mass might be placed on completions like “landscapes”, “cities”, “people”, etc. which are consistent with the lakes being beautiful. There are simply many valid words that could fit in this spot.

The key observation is that when a language model is uncertain about the next token, its uncertainty is a mix of epistemic uncertainty—reflecting the model’s ignorance—and aleatoric uncertainty—reflecting the inherent unpredictability of text. When our model was uncertain about “Finland”, this was primarily epistemic uncertainty—there was a knowable correct answer. When it was uncertain about “lakes”, its uncertainty was primarily aleatoric. A viable solution for mitigating hallucinations cannot rely simply on the model’s total uncertainty—it is epistemic uncertainty which matters. In our new work, we thus study the problem of distinguishing epistemic from aleatoric uncertainty (i.e., “knowing what is knowable”) in the outputs of language models. While prior works on estimating epistemic uncertainty have primarily limited their scope to small models and/or structured question-answering settings, we set out to identify epistemic uncertainty in larger models on free-form unconstrained text.

We show that supervised linear probes trained on a language model’s internal activations can achieve high accuracy at classifying epistemic versus aleatoric uncertainties, even when the probes are evaluated on unseen text domains (probes trained on Wikipedia text, for example, generalize well to code data). Going further, we provide a completely unsupervised method for the same tasks that outperforms naive baselines.

One way to define the difference between epistemic and aleatoric uncertainty is that aleatoric uncertainty is inherent to the randomness in language, while epistemic uncertainty is “in the eyes of the beholder.” As the quantity of training data and computation time increases, models will learn more of what is knowable, and epistemic uncertainty will recede. In other words, as language models become bigger and trained for longer, they become better proxies for the “true” distribution. Specifically, we posit a setting where we have access to a relatively small language model of interest (say, LLaMA 7B), as well as a more knowledgeable reference language model (say, LLaMA 65B, or, better, a model at the level of GPT-4). We will refer to the first model as the small model and the second model as the large model.

The goal is to be able to identify tokens where the small model has high epistemic uncertainty. The large model serves as a proxy for the ground truth, providing a way to obtain (imperfect, but still meaningful) “epistemic uncertainty labels” that can be used to evaluate different approaches. Our supervised approach will use the large model to train simple probes on the activations of the small model, but will not have access to it at inference time. Our unsupervised approach will not have access to the large model at all.

To generate uncertainty labels for a set of tokens, we use both models to generate conditional predictions at each token and flag cases where the two models significantly disagree on the entropy of the next token.

Tagging Method:

Tagging Example:      

Oppenheimer obtained his Doctor of Philosophy degree in March 1927, at age 23, supervised by Max(Max/Arnold/Albert) Born. After the oral exam, James Franck, the professor administering it, reportedly said, “I(I/This/You)’m glad that’s over. He was on the point(ver/fac/br) of question(saying/asking/being)ing me(me/the/him).” Oppenheimer published more than a dozen papers while in Europe, including many important contributions to the new field of quantum mechanics. He and Born(Born/his/Fran) published a famous paper on the Born(quantum/theory/electron)-Oppenhemer approximation, which separ(is/was/describes)ates nuclear(the/electronic/out) motion from electronic motion in the mathematical(calculation/study/quantum) treatment(treatment/description/form) of molecules, allowing nuclear motion to be neglected to(in/./and) simplify(a/an/first) calculations.

We’ve highlighted this passage from Wikipedia using LLaMAs 7B and 30B according to the difference between their predictive entropies at each token. Black denotes no meaningful difference (i.e., < 0.2), and red denotes the largest difference (i.e., > 2.0). In cases where two models disagree the most, we’ve also inserted in parentheses the top three token predictions from the small model. Qualitatively, we can see that tokens highlighted in red above (large disagreements) tend to include factual or otherwise deterministic information (the name of Oppenheimer’s advisor, the content of his paper with Born, tokens in a quotation the large model seems to be familiar with). 

In general, if the large model is capable enough, we expect tokens where the small model is uncertain while the large model has near-zero entropy to be instances where the small model uncertainty is purely epistemic. Other tokens with a large entropy difference would be mixtures of epistemic and aleatoric uncertainty. To simplify the setup, we focus on the former kind: Among all the tokens that the small model is uncertain about, we create a binary classification task: labeling tokens where the large model has low entropy with “0” and all other tokens “1”.

There are obvious limitations to this contrastive setup, which stem from the fact that large models are only proxies for the true language distribution. The quality of our label depends on the large model used for tagging. If the large model exhibits epistemic uncertainty in its own right, “epistemic” tokens could slip through the cracks. This issue can be addressed by simply scaling up the large model further. And in practice, we find that our probes make accurate predictions on the classification task anyway.

Supervised probes

In the supervised setting, we train linear classifiers on a small model’s “next-token” activations to predict uncertainty labels. Empirically, we find that activations from the middle layers work the best (sometimes by large margins). Our probes are mostly trained using a set of Wikipedia articles that are new enough that they aren’t present in the models’ training data. Our models are selected from the LLaMA, Llama 2, and Pythia model families.

To make sure that our probes are not just learning trivial heuristics, we perform a few interventions on our training and evaluation sets.

First, we note that small model entropy and large model entropy tend to be very heavily correlated (see log-colored heatmaps above). The high correlation means that it is possible for a small-model probe to predict the large model’s entropy at any given token with high accuracy simply by outputting the entropy of the small model at that token. Second, the entropy at a token is often heavily influenced by the previous token; tokens following a period, for example, tend to have higher entropy according to both models. To prevent the probe from learning the two trivial cases mentioned, we train individual probes on 1) a narrow band of the small model’s entropy (sample band depicted in green) and 2) balance the two classes for each “previous” token.

We run some simple baselines as sanity checks. BET (best entropy threshold) is the best classifier that simply thresholds the small model’s entropy on a given evaluation set. BET-FT uses the same entropy after the small model’s language modeling head is fine-tuned on distributions output by the large model (to control for the effects of the fact that the probes are being trained on data slightly out of the training distribution of the small model).

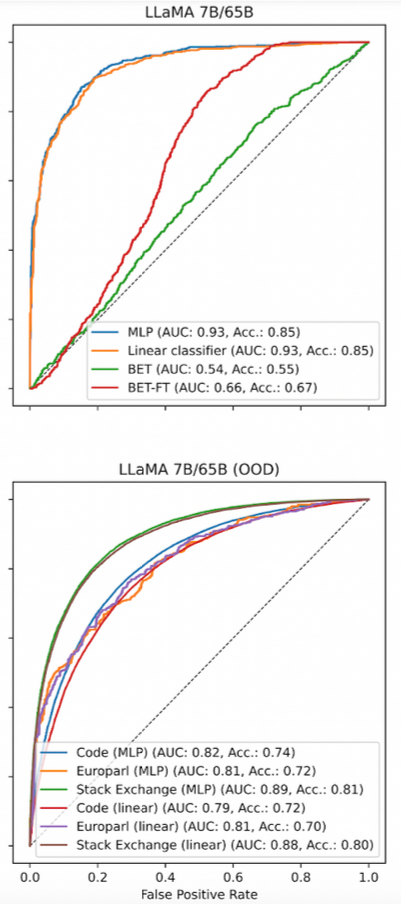
Overall, we find that the probes (denoted “MLP” and “Linear classifier” in the above plots) are extremely effective, and greatly outperform both baselines in all cases. We provide ROC curves for a handful of classifiers above. Probes trained on Wikipedia data are almost perfect classifiers of Wikipedia tokens (top plot), and they are also surprisingly effective when evaluated on radically different text distributions, such as code, foreign language text (Europarl), and Stack Exchange forum posts without any additional training (bottom plot).

The fact that the linear probe in particular performs so well means that notions of epistemic uncertainty are linearly represented in the activations of LLMs. At first we thought that this finding might be simply reflecting the fact that LLMs form rich representations of language that are useful in general—perhaps this richness is sufficient to encapsulate aspects of language that are correlated with the epistemic/aleatoric distinction. But the impressive transfer performance of the probes when they are trained on one domain and evaluated on a completely different domain suggests that they might not be merely learning correlations—the LLM representations may “natively encode” epistemic uncertainty in some mysterious way. We’re not sure what’s going on here!

Unsupervised approach

The supervised probing results are promising, but in order to implement them in practice, when training the probe one needs access to a more powerful model than the model one actually is going to deploy. This does reflect some real-life situations—e.g., deploying a small model for efficiency reasons, or because the most powerful models are proprietary. We now consider whether it is possible to perform uncertainty disentanglement on the most powerful models available. In order to study this, we will still consider the small model to be the one we will deploy, but now we will not allow access to the large model at all except for evaluation.

In particular, we propose an unsupervised method inspired by the phenomenon of in-context learning. Large language models are adept at in-context learning: while they do store information directly in their parameters, they can also work with new facts and even new tasks presented to them entirely in-context.

Copying information from the context makes more sense in some cases than others. Suppose the model needs to fill in the blank in “Vänern is the largest lake in the country of __”, and suppose the full sentence “Vänern is the largest lake in the country of Sweden” occurred earlier in the context. Then, even if the model is initially uncertain about the location of Vänern, we expect the model to predict “Sweden” for the second occurrence as well as long as it knows there is only one correct answer. Alternatively, suppose the model needs to complete “Sweden has beautiful __”, given that “Sweden has beautiful landscapes” appeared earlier in the context. In this case, the model may still place significant probability on completions besides “landscapes”, because they are not incompatible with the first occurrence. Our unsupervised method relies on the hypothesis that language models are capable of this sort of selective in-context learning, and lean on in-context information more heavily when their uncertainty is primarily epistemic.

Unsupervised uncertainty classification (synthetic example)

To show that language models can develop that capability, we first consider language modeling in a synthetic setting. We construct binary question/answer pairs that consist of the following:

1. An “epistemic/aleatoric” bit, indicating whether the question is aleatoric or not.
2. A question ID, of some length k
3. A single answer bit

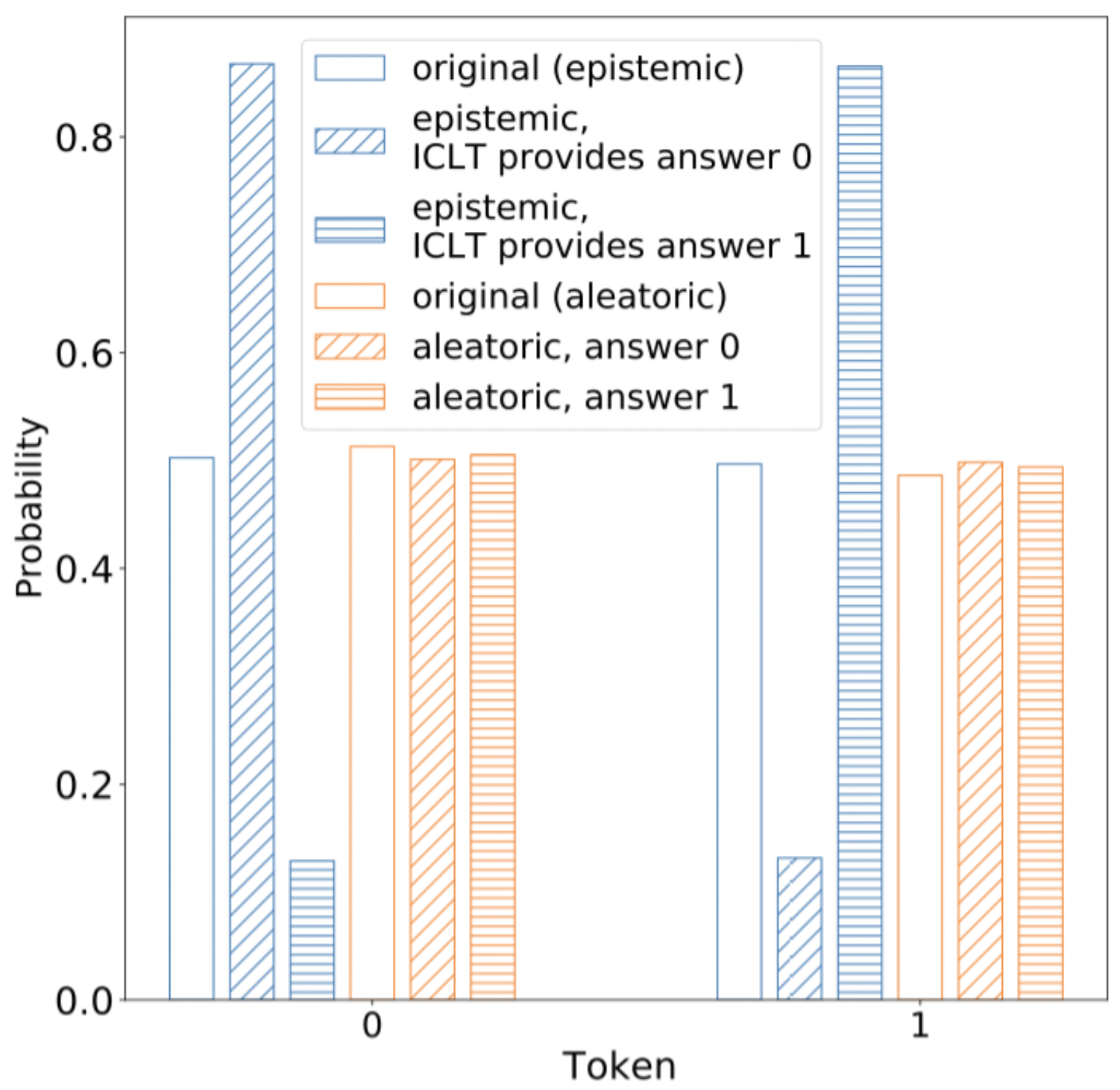
Crucially, we generate the answer bit differently for “epistemic” vs “aleatoric” questions. For epistemic questions, we sample an answer bit uniformly at random in advance and then fix it—every time that question appears, it has the same answer. Epistemic questions can be memorized. Aleatoric questions, on the other hand, have newly sampled random answers at every occurrence.

We train a nanoGPT model (~100M parameters) to answer questions of this form in a few shot setting and then evaluate it on held-out data. Our intuition is that the model should always start with a 50/50 prediction for questions of both types—this is the correct prediction for aleatoric questions, and the model has no way to know the answers to the unseen epistemic questions in the evaluation set. After we provide it with hints in-context, however, we expect it to update its answers for epistemic questions, but not aleatoric questions. That is indeed what we see:

Unsupervised uncertainty classification (real example)

In the synthetic setting, it is simple to determine if a token is “aleatoric” or “epistemic”; the model only needs to attend to the first bit of the question, and can change its behavior accordingly. Is this possible in natural language, where this information—insofar as tokens are even strictly “aleatoric” or “epistemic” at all—is much more diffuse? If so, do large language models learn to respect the distinction?

To some extent, the answer to both questions seems to be “yes”! We test them with the following technique, which we term the “In-Context Learning Test,” or ICLT for short. Here’s a walkthrough of how it works:

In–Context Learning Test Procedure using example “Vänern is the largest lake in __”:

Suppose “Vänern is the largest lake in __” is the original prompt. 

Step 1: We first use the small model to generate candidate next-token predictions from the original prompt. The small model outputs the follow three predictions with probabilities in descending order: Sweden (p=0.4), Norway (p=0.4), Europe (p=0.2)

Step 2: 

• We add each of the three tokens (Sweden, Norway, Europe) to the original prompt to form three completed prompts.
  • Completed prompt 1: “Vänern is the largest lake in Sweden.” 
  • Completed prompt 2: “Vänern is the largest lake in Norway.” 
  • Completed prompt 3: “Vänern is the largest lake in Europe.” 

• For all three completed prompts, we then prepend it to the original prompt, to form a new repeated prompt with in-context information. We insert a separator token in between repetitions to mimic how independent documents are packed into a single context during the model’s pre-training.
  • Repeated prompt 1: “<BOS>Vänern is the largest lake in Sweden.<BOS>Vänern is the largest lake in __” 
  • Repeated prompt 2: “<BOS>Vänern is the largest lake in Norway.<BOS>Vänern is the largest lake in __” 
  • Repeated prompt 3: “<BOS>Vänern is the largest lake in Europe.<BOS>Vänern is the largest lake in __” 

• We use the small model to separately generate next token predictions using the three repeated prompts. The extra in-context information may alter the model’s prediction. The small models’ outputs from the three repeated prompts might be:
  • Repeated prompt 1 generation: Sweden (p=0.9), Norway (p=0.05), Europe (p=0.05)
  • Repeated prompt 2 generation: Sweden (p=0.05), Norway (p=0.9), Europe (p=0.05)
  • Repeated prompt 3 generation: Sweden (p=0.30), Norway (p=0.40), Europe (p=0.30)
• In other words, after seeing the information provided, the model becomes more confident in predicting certain tokens, and less in others. 

Step 3: We compute entropy for all the repeated prompt generations, and use the minimum of these entropies as a scalar value for solving the classification task (i.e., predicting the large model’s uncertainty). In particular, we learn a simple threshold classifier on this scalar.

Let’s visualize the results of the ICLT on two hand-picked prompts. 

The first (“epistemic-like”) prompt is: “36-42 Coney Street is a historic terrace in the city centre of __”, for which there is a single correct answer—if the model has a lot of uncertainty, it is mostly epistemic.

For our second (“aleatoric-like”) prompt we will use “Bulgurluk is a village Genç Distric, Bingöl Province, Turkey. The village is __”, for which there is plenty of aleatoric uncertainty.

In the plot, we first show the original predicted probabilities in gray bars for the top 10 predictions. We then show the probability of the model repeating the same token when prompted with “<BOS>original prompt + token. <BOS>original prompt” . On the “epistemic-like” prompt, probabilities rise significantly, signifying that the model is “copying” from its input. In the aleatoric case, the model is more reluctant to modify its predictions based on the new information provided in the context.

We include some hand-picked examples above. Gray bars show the original predicted probabilities for each token. Colored bars show the probability of the same tokens in new prompts that include those tokens as hints. On the “epistemic-like” prompt, probabilities rise significantly, signifying that the model is “copying” from its input. In the aleatoric case, the model is more reluctant to modify its predictions.

Applying ICLT to LLaMA models as a classifier for the same uncertainty labels we used in the supervised case, we find that it outperforms naive entropy baselines on the Wikipedia test set (AUC ~ 0.70 compared to ~ 0.55). This is a proof-of-concept result that unsupervised uncertainty disentanglement might be possible for real LLMs.

However, it fails on Pythia models, which seem to be more prone to repeating information no matter what. In the future, we plan to test the method on more diverse models and determine more precisely when it fails.

Conclusion

In summary, we’ve introduced 1) a new way to label different types of uncertainty in unconstrained text and 2) simple methods to predict those labels, including a completely unsupervised approach. More work needs to be done before they can be transformed into practical tools to detect uncertainty in the wild—specifically, the recall of our classifiers on realistic, unbalanced data is still too low. If that point can be reached, however, they could become part of a solution for making language models more transparent about what they know and less susceptible to hallucinations. For more about our setup, methods, and findings, check out our paper!